Основные понятия

Ряд, членами которого являются функции от х, называется функциональным:

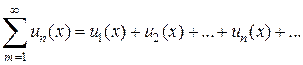(1)

Придавая х определенное значение 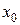, мы получим числовой ряд

,

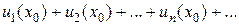который может быть как сходящимся, так и расходящимся.

Если полученный числовой ряд сходится, то точка 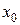называется точкой сходимости ряда (1); если же ряд расходится – точкой расходимости функционального ряда.

Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется его областью сходимости.

В области сходимости функционального ряда его сумма является некоторой функцией от х: 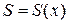. Определяется она в области сходимости равенством

 

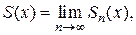
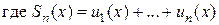– частичная сумма ряда.

 

Пример 1. Найти область сходимости ряда .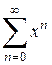

Решение. Данный ряд является рядом геометрической прогрессии со знаменателем Следовательно, этот ряд сходится при 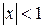, т. е. при всех ; сумма ряда равна :

 

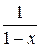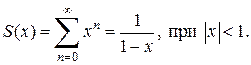
Пример 2. Исследовать сходимость функционального ряда

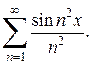
Решение. Составим ряд из абсолютных величин членов исходного ряда

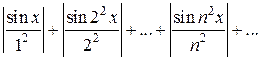(2)

Так как при любом 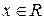имеет место соотношение 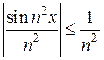, а ряд с общим членом 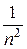сходится (обобщенный гармонический ряд, р =2 >1), то по признаку сравнения ряд (2) сходится при 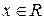. Следовательно, исходный ряд абсолютно сходится при всех .

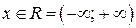Среди функциональных рядов в математике и её приложениях особую роль играет ряд, членами которого являются степенные функции аргумента х, т. е. так называемый степенной ряд:

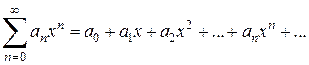(3)

Действительные (или комплексные) числа 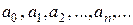называются коэффициентами ряда (3), 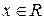– действительная переменная.

Ряд (3) расположен по степеням х. Рассматривают также степенной ряд, расположенный по степеням 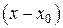, т. е. ряд вида

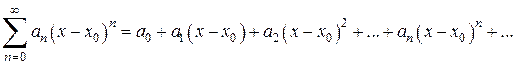, (4)

где 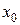– некоторое постоянное число.

Ряд (4) легко приводится к виду (3), если положить Поэтому при изучении степенных рядов может ограничиться степенными рядами вида (3).