Взаимное расположение прямой и плоскости
Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость g и установим относительное положение двух прямых а и в, последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a (рис.50).
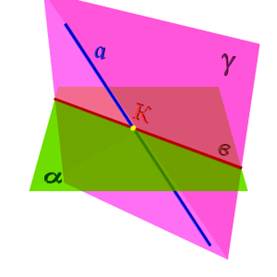
Рисунок 50. Метод вспомогательных секущих плоскостей
Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости a, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость a.
Таким образом возможны три случая относительного расположения прямой и плоскости:
· Прямая принадлежит плоскости;
· Прямая параллельна плоскости;
· Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости.
Рассмотрим каждый случай.