Различные виды приближений. Интерполяция и аппроксимация.

Аппроксимация заключается в том, что используя имеющуюся информацию по f(x) можно рассмотреть другую функцию ц(ч) близкую в некотором смысле к f(x), позволяющую выполнить над ней соответствующие операции и получить оценку погрешность такой замены. ц(х)- аппроксимирующая функция. Интерполяция (частный случай аппроксимации)

Интерполяция – один из способов аппроксимации данных. В простейшем (одномерном) случае задача интерполяции [1-3] состоит в следующем: заданы точки (x_i, y_i), 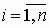и требуется найти функцию 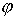(x), которая проходит через эти точки (см. рис. 1),

т.е.

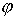(x_i)= y_i , 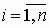. (1)

Точки (x_i, y_i) называют узлами интерполяции, а функцию 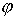(x) – интерполирующей функцией или интерполянтом. Вид функции 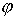(x) определяет способ интерполяции. На практике в качестве интерполирующей функции 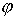(x) часто используются алгебраические полиномы различного вида, так как полиномы легко вычислять, дифференцировать и интегрировать. При этом интерполяция носит название полиномиальной.