Критерий Лапласа

Если игрок А не располагает объективной информацией об вероятностях q_j состояний природы Пj и считает в равной степени правдоподобными все состояния, то их вероятности полагают одинаковыми и равными . Этот прием называют принципом недостаточного основания Лапласа.

Отсюда вытекает и критерий Лапласа, в соответствии с которым оптимальной считается чистая стратегия, обеспечивающая максимальный средний выигрыш игрока А при равенстве всех вероятностей.

В этом случае показатели эффективности каждой стратегии рассчитываются по формуле:

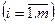, а цена игры равна:

При использовании критериев Байеса и Лапласа предполагается, что ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:

· Вероятности появления состояний Пj известны и не зависят от времени;

· Решение реализуется (теоретически) бесконечно много раз;

· Для малого числа реализаций допускается некоторый риск.

При достаточно большом числе реализаций среднее значение постепенно стабилизируется, поэтому при полной (бесконечной) реализации какой-либо риск практически исключен.