Статистические методы оценки

 

Доходность актива это случайная величина. Рассчитать ожидаемое значение доходности финансового актива можно двумя способами. Первый состоит в том, чтобы на основе прошлых данных статистик доходности актива рассчитать ее среднеарифметическое значение :

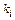- фактическая доходность актива в i-том периоде;

n –число периодов наблюдения.

Второй подход заключается возможного будущего вероятностного распределения доходности актива. В этом случае ожидаемая доходность определяется как среднеарифметическая взвешенная, где весами выступают вероятности каждого события.

Основополагающими мерами риска финансового актива являются такие показатели как стандартное отклонение и дисперсия его доходности.. В качестве синонима понятия «стандартное отклонеие» используют так же термин «волатильность». Стандартное отклонение и дисперсия доходности актива о степени возможного разброса его фактической доходности вокруг его средней доходности. Данные меры риска можно определить на основе его прошлых данных статистики его доходности.

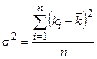
Величина σ² является дисперсией доходности акции за год. Размерность дисперсии представляет собой квадрат доходности. Показателем такой размерности не всегда удобно пользоваться, поэтому из дисперсии извлекают квадратный корень и получают стандартное отклонение

Дисперсию актива можно рассчитать и на основе прогнозов инвесторов в отношении конъюнктуры будущего периода. В этом случае инвестор оценивает возможные сценарии ее развития на этой основе он прогнозирует значения будущих доходностей актива и задает им субъективные вероятности

Непрерывная случайная величина – та, которая может принимать бесконечное число возможных результатов. (рентабельность активов)

Количество возможных значений доходности может быть бесконечно велико: 3,8 %, 3,81 %, 3,095 % - в зависимости от количества знаков после запятой, допускаемого при измерении. В этих обстоятельствах нет никакого смысла в нахождении вероятности значения доходности равной 3,81 %. Имеет смысл только нахождение вероятности того, что случайная переменная примет значение на каком-либо определенном интервале – между 3,81 % и 3,82 %.

Чтобы найти ожидаемую величину необходимо интегрировать функцию плотности вероятности:

Математическое ожидание непрерывной случайной величины:

Дисперсия и среднее квадратичное отклонение соответственно:

 

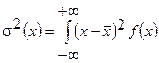
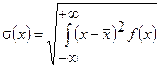
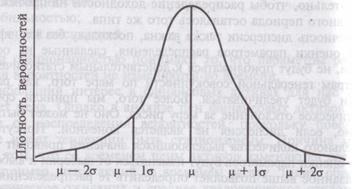
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

 

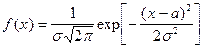
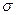Нормальное распределение определяется двумя параметрами: математическим ожиданием и средним квадратическим отклонениеми на графике представляет собой симметричную колоколообразную кривую Гаусса, имеющую максимум в точке, соответствующей значению 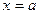, а пр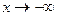и и 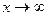асимптотически приближающуюся к оси абсцисс. Точка перегиба кривой находится на расстоянии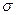от центра распределения. Изменение параметра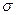приводит к изменению степени растяжения кривой: с уменьшением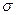кривая вытягивается в центре и быстрее приближается к оси абсцисс при удалении от центра.