Множественная и частная корреляция.

Многофакторная система требует множество показателей тесноты связей, имеющих разный смысл и применение. Основой измерения связей факторными признаками является матрица парных коэффициентов корреляции, которые определяются по формуле:

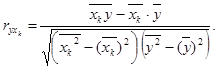
На основе парных коэффициентов корреляции вычисляется наиболее общий показатель тесноты связи всех входящих в уравнение регрессии факторов с результирующим признаком – коэффициент множественной детерминации как частное от деления определителя матрицы на опрделитель матрицы ∆: , где

;

.

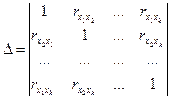Этим способом можно определить коэффициент детерминации, не вычисляя расчетных значений результативного признака для всех единиц совокупности, если совокупность состоит из сотен и тысяч единиц.

Если же совокупность небольшая, то можно применять индекс корреляции для определения адекватности описания связи между рассмотренными в уравнении множественной регрессии факторными и результативным признаками:

.

Для определения тесноты связи двухфакторного уравнения регрессии вычисляются парные коэффициенты корреляции , и по формулам:

где ; ; .

После этих вычислений находят коэффициент множественной корреляции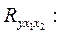

 

Этот коэффициент находится в пределах от 0 до 1. Он оценивает тесноту связи показателя у с двумя факторами х₁, х₂ одновременно.

Теснота связи между результативным признаком и одним из факторов характеризуется с помощью частных коэффициентов корреляции 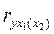и где

 

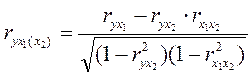
Аналогичную формулу можно записать для :

.