Бином Ньютона, треугольник Паскаля

Рассмотрим бином (a+b)ⁿ. Если раскрыть скобки, привести подобные, то получившиеся сумма состоит из слагаемых вида aⁱb^n-i с некоторыми числовыми коэффициентами. Например: (a+b)²=a²b⁰+2ab+a⁰b². В общем случае можно записать 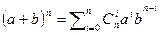, где - числовой коэффициент. Из тождества (a+b)ⁿ=(a+b)(a+b)^n-1 выводим равенства и , которые позволяют строить треугольник Паскаля. Приведём первые его 4 строки . Число, расположенное в треугольнике Паскаля на пересечении строки n и столбца m, равно

· 1, если m=0, или m=n,

· сумме элементов предыдущей строки, расположенных в столбцах m и m-1, если .

Таким образом, элементы треугольника Паскаля суть биномиальные коэффициенты. В частности .

Обозначим через произведение натуральных чисел от 1 до n. Для удобства обозначений положим .

Теорема 1.1 Биномиальный коэффициент вычисляется по формуле .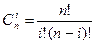

Доказательство проводится индукцией по n. При n=1 утверждение очевидно. Пусть оно верно при n-1. Покажем его справедливость для n. Если m=0, то . Если m=n, то . Если , то 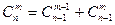. По предположению индукции . Теорема доказана.