Расчет равновесной концентрации электронов и дырок

Для расчета равновесной концентрации электронов и дырок необходимо знать плотность разрешенных энергетических уровней и вероятность их заполнения электронами. В квантовой физике доказывается, что вблизи краев энергетических зон плотность разрешенных энергетических уровней N(E) подчиняется параболическому закону.

Для зоны проводимости

. (3.1)

Для валентной зоны

.(3.2)

Вероятность заполнения разрешенных уровней определяется функцией Ферми-Дирака:

. (3.3)

Обычно в полупроводниках разность Е–Е_F более чем в три раза превышает величину kT, поэтому единицей в знаменателе формулы (1.32) можно пренебречь. Тогда вероятность заполнения энергетических уровней в зоне проводимости будет равна

. (3.4)

Вероятность отсутствия электрона на энергетическом уровне в валентной зоне, то есть вероятность возникновения дырки, будет равна

. (3.5)

Энергетическая плотность электронов равна

, (3.6)

Концентрации электронов равна

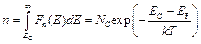. (3.7)

Здесь — эффективная плотность состояний в зоне проводимости.

Энергетическая плотность дырок равна

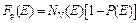, (3.8)

а их концентрация равна

. (3.9)

Здесь — эффективная плотность состояний в валентной зоне.

Графики N(E), p(E) и F(E) для собственного полупроводника представлены на рис.3.1.

Рис.3.1

 

В собственном полупроводнике n_i=p_i, следовательно,

.

Логарифмируя и решая относительно E_Fi, получаем:

.

Величина значительно меньше, чем , поэтому , то есть уровень Ферми в собственном полупроводнике расположен приблизительно посередине запрещенной зоны.

В собственном полупроводнике , поэтому

. (3.10)

Чем больше ширина запрещенной зоны, тем меньше концентрация собственных носителей заряда. С повышением температуры концентрации электронов и дырок возрастают по экспоненциальному закону.

В электронном полупроводнике концентрация электронов в основном обусловлена переходом электронов с энергетических уровней Е_D на энергетические уровни зоны проводимости. Так как N_D>> n_i, то из (3.7) следует, что в электронном полупроводнике уровень Ферми E_Fn должен быть расположен выше середины запрещенной зоны (рис.3.2,а). При этом график р(Е) на рис 3.1 должен сдвинуться вверх, ординаты графика F_n (Е) увеличиться, а ординаты графика F_p (Е) уменьшиться. Следовательно,

.

 

а ) б)

Рис.3.2

Поэтому уравнение (3.7) можно представить в виде:

. (3.11)

Учитывая, что , уравнение (1.9) принимает вид:

. (3.12)

Умножая n_n на p_n, получаем:

. (3.13)

Таким образом, при любой концентрации примесей произведение концентраций электронов и дырок в электронном полупроводнике остается постоянной величиной.

На практике в области рабочих температур можно считать, что все доноры ионизированы, то есть n_n=N_D. Тогда из (13.13) следует, что , то есть, чем выше концентрация доноров, тем меньше концентрация дырок. Если n_n=N_D, то из уравнения (3.11) можно определить положение уровня Ферми в электронном полупроводнике:

. (3.14)

В дырочном полупроводнике концентрация дырок в основном обусловлена переходом электронов с энергетических уровней валентной зоны на энергетический уровень акцепторов. При этом уровень Ферми должен быть расположен ниже середины запрещенной зоны (рис.3.2,б), график р(Е) сдвинут вниз, ординаты графика F_р(Е) должны возрасти, а ординаты графика F_n (Е) уменьшиться. Следовательно,

,

и уравнение (3.9) принимает вид:

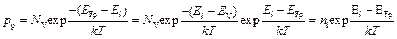. (3.15)

С учетом того, что , уравнение (3.7) принимает вид:

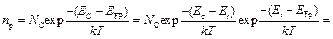
. (3.16)

Перемножая p_p и n_p, получаем

(3.17)

Если все примесные атомы ионизированы, то p_p≈ N_A. Тогда из (3.17) следует, что

,

то есть, при увеличении концентрации акцепторов уменьшается концентрация электронов

. Уравнение (3.15) позволяет определить положение уровня Ферми в дырочном полупроводнике при p_p=N_A:

. (3.18)

Концентрация носителей заряда зависит от температуры (рис.3.3). При T=0 K все валентные электроны заняты в ковалентных связях, валентная зона полностью заполнена электронами, а в зоне проводимости электроны отсутствуют. При повышении температуры происходит ионизация примесных атомов, поэтому концентрация основных носителей заряда возрастает (участок 1). При температуре около100 К, практически все примесные атомы ионизированы, поэтому в интервале температур от 100 К до примерно 400 К (участок 2), концентрация основных носителей заряда сохраняется приблизительно постоянной и равной концентрации примесей. Некоторое увеличение концентрации в этом интервале температур объясняется тепловой генерацией электронов и дырок. При температуре выше 400 К возрастает скорость тепловой генерации, вследствие чего концентрация основных носителей заряда увеличивается (участок 3) и различие между концентрациями основных и неосновных носителей заряда уменьшается, полупроводник постепенно приобретает свойства собственного полупроводника. Поскольку с ростом температуры происходит возрастание концентрации основных носителей заряда, то в электронном полупроводнике уровень Ферми опускается вниз, а в дырочном поднимается вверх, приближаясь к середине запрещенной зоны.

Концентрация неосновных носителей заряда, с ростом температуры возрастает по экспоненциальному закону, причем она растет быстрее, чем концентрация собственных носителей. Это следует из уравнений (13.13) и (3.17), в которых надо принять n_n=N_D и p_p=N_A, тогда

. (3.18)

. (3.19

Показатели степени экспоненты в (3.18) и в (3.19) вдвое больше показателя степени экспоненты в (3.10), следовательно, концентрации n_p и p_n более сильно зависят от температуры, чем концентрация n_i