Турбулентный пограничный слой.

Профиль осредненной по вре­мени скорости и(у) жидкой частицы при ее турбулентном движе­нии в пограничном слое около гладкой полубесконечной пластины характеризуется тремя размерными параметрами: кинематическим коэффициентом вязкости , динамической скоростью u_*=и вертикальным (нормальным к пластине) масштабом всего те­чения δ. Эти параметры позволяют выявить два линейных масшта­ба: v/u_* и δ. Первый из них содержит молекулярную вязкость и поэтому можно считать, что он отражает особенности течения вблизи стенки, второй характеризует течение во внешней области пограничного слоя. На основании теории размерности можно записать две эквивалентные зависимости:

= (6.3)

= (6.4)

Будем считать число Рейнольдса течения достаточно большим, таким, что Re δ=δu_*/>>l. Следовательно, параметр δu_*/в функ­циональных зависимостях (6.3), (6.4) можно заменить беско­нечностью или просто не считать его переменным и не рассматри­вать.

Тогда при у<<δ из (6.3) получим закон стенки

= (6.5)

или

u⁺(y)=f₃(y⁺) (6.6)

где u⁺(y) = u(y)/u_*; y⁺=

=

В области y из (6.4) получим закон дефекта скорости:

(6.7)

(6.8)

 

где ;

Предположим, что существует область перекрытия обоих за­конов (6.5) и (6.7). Приравняем их между собой и домножим на у. В результате получим

Левая часть равенства зависит лишь от независимой перемен­ной у+, а правая— только от. Следовательно, левая и правая ча­сти должны быть равны некоторой константе А. Таким образом можно записать

Отсюда следует, что в зоне перекрытия распределение скоро­сти подчиняется логарифмическому закону:

(6.9)

(6.10)

На основании экспериментальных данных A=1/ 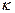, где 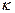=0,4 —универсальная константа Кармана, В₁ = 2,4, В = 5,56.

Логарифмический закон стенки, разумеется, нельзя распро­странить на непосредственную окрестность стенки (). В этой области профиль скорости можно получить непосредственно из уравнений ламинарного пограничного слоя. В самом деле, в окре­стности стенки молекулярная вязкость значительно превосходит турбулентную, так что последней можно пренебречь. Поэтому

;

Отсюда следует , p=const.

Граничными условиями будут: при y=0 u=0, .

Таким образом,

или

(6.11)

Как видим, профиль скорости в ламинарном (вязком) подслое при безградиентном течении является линейным.

Безразмерная граница ламинарного подслоя является основ­ной эмпирической постоянной пристенного турбулентного тече­ния. Многочисленными измерениями установлено, что

, где (6.12)

 

С физической точки зрения эту величину можно трактовать как критическое число Рейнольдса, при котором ламинарный подслой теряет устойчивость. С математической точки зрения она опреде­ляется как точка пересечения линейного и логарифмического за­конов изменения скорости в пристенной области. В действительно­сти переход от ламинарного подслоя к турбулентному ядру осу­ществляется плавно в пределах буферной зоны.

Ламинарный подслой занимает весьма малую часть погранич­ного слоя: 0,001...0,01. Логарифмический закон стенки и закон де­фекта скорости хорошо описывают профиль скорости до ~0,2.

Для инженерных целей полезны методы, которые дают результат в замкнутых формулах. Обратимся к интегральному соотношению импульсов. В случае пластины и (2.74) приобретает наиболее простой вид:

 

(6.13)

Вместе с тем уравнение содержит две неизвестные величины: **(x) и (x). Следовательно, необходимо иметь какое-либо до­полнительное соотношение. Как правило, это соотношение полу­чают из экспериментов.

Прежде всего, эмпирическим путем можно установить связь между и **. Примером может служить степенной закон сопро­тивления Фолкнера:

(6.14)

Введем обозначения:

,

и перепишем уравнение (6.13) в форме

и далее с учетом (6.14) придадим ему вид

После интегрирования получим

Будем считать, что турбулентный пограничный слой начинает­ся с передней кромки пластины, т. е. при х=0 ** = 0. Отсюда следует, что С=0.

Итак,

Re** =0,0153 (6.15)

Или

(6.16)

Как видим, толщина потери импульса подчиняется примерно линейному закону в зависимости от х. В ламинар­ном пограничном слое , т. е. величина ** вдоль по потоку растет мед­леннее.

Найденное значение ** подставим в исходный закон сопротив­ления Фолкнера (6. 14) и определим местный коэффициент со­противления:

(6.17)

Полный коэффициент сопротивления пластины длины L и еди­ничной ширины получится интегрированием:

(6.18)

где

Re_L=

Значение местного коэффициента трения C_f падает вдоль пла­стины. Передняя кромка вновь, как и в случае ламинарного по­граничного слоя, является особой точкой.

Более точной и поэтому более употребитель­ной для турбулентного течения является формула Коулса, объеди­няющая логарифмический закон и закон следа:

(6.19)

где W(y/) = 1-cos— функция следа. Для удобства вычисле­ния интервалов при использовании интегральных соотношений функцию следа иногда представляют в виде степенных многочле­нов, в частности в виде

П(х)-параметр Коулса, в общем случае отражающий влияние градиента давления. В случае пластины градиент давления отсут­ствует и потому

П(х)= const=0,55; Х₀=0,4; B=5,1.

Еще Прандтль использовал логарифмический про­филь скорости для расчета местного и полно­го коэффициента трения пластины. Выкладки получились доволь­но сложными, и результаты вычислений были представлены в ви­де таблиц. В дальнейшем Шлихтинг предложил аппроксимационную зависимость, которая именуется формулой Прандтля — Шлихтинга:

(6.20)

Считается, что она дает наиболее точные результаты во всем практическом диапазоне чисел Рейнольдса, включая предельно большие значения.

Расчетные значения C_Fx, полученные по формуле Блазиуса (6.2) (кривая 1), по формуле Прандтля — Шлихтинга (6.20) (кривая 2), показаны на рис. 6.3.

Рис. 6.3 наглядно иллюстрирует различный характер зави­симости коэффициента сопротивления от числа Рейнольдса при различных режимах

течения: ламинарном или турбулентном.

Рис. 6.3 Зависимость коэффициента сопротивления от числа Рейнольдса.