Простая разветвленная сеть

 

Основными задачами можно считать: определение концевых расходов Q₁ и Q₂ при заданном напоре в начальном сечении или определение напора при заданных концевых расходах Q₁ и Q₂. В качестве примера рассмотрим первую задачу. Составим уравнение Бернулли для потока по линии от начального сечения магистральной трубы до выходного сечения первой ветви (вдоль линии 0 – А - 1), а затем до выходного сечения второй ветви (вдоль линии 0 – А – 2).

Рис. 6.6.

В первом случае

(6.35)

а во втором

(6.36)

где - потери напора на участке 0 – А (на магистрали), на первой и второй ветвях.

Обозначим расход в первой ветви Q_1, а во второй Q₂. Очевидно в магистрали расход будет равен их сумме (Q+Q₂). Имея это ввиду, запишем равенства (6.35) и (6.36) иначе (пренебрегая скоростными напорами на выходе).

Потери напора на магистральной линии

или обозначив

получим

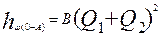
Аналогично

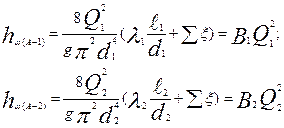
Коэффициенты В; В₁; В₂, очевидно связаны с удельным сопротивлением трубопровода. Действительно

но

поэтому

и соответственно

При отсутствии же местных сопротивлений или пренебрежении ими по сравнению с потерями по длине, т.е. для длинных трубопроводов:

B=AL=S; B₁=A₁=S₁; B₂=A₂=S₂.

В условиях квадратичного закона сопротивлений коэффициенты и , а следовательно, В, В₁ и В₂ вычисляются однозначно, и их можно считать известными. Тогда исходные уравнения (6.35) и (6.36) перепишутся следующим образом

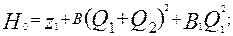(6.37)

(6.38)

Решая эти два уравнения, находим Q₁ и Q₂.

В неквадратичной области сопротивлений расчеты можно производить методом последовательных приближений с использованием поправки на неквадратичность .