Физическое моделирование
Математическое моделирование представляет физические процессы в упрощенном идеализированном виде. В прежнее время, когда вычислительные возможности были сильно ограничены, основу изучения процессов формирования микроклимата составляло физическое моделирование .
Физическое моделирование осуществляется в натурных условиях и на геометрически подобных моделях. Натурные исследования проводят на действующих объектах. Возможны разовые обследования и длительные наблюдения (мониторинг) за объектом.
Изучение свойств объекта в натурных условиях имеет преимущество достоверности. Однако в натурных условиях затруднительно установить закономерности тех или иных процессов из-за большого числа помех случайного характера. Этот недостаток скрадывается при длительном наблюдении объекта. При последующем осреднении результатов длительного наблюдения случайные факторы, действующие в ту или иную сторону, взаимно погашаются, проявляя таким образом основную закономерность процесса.
В настоящее время имеется большое разнообразие измерителей параметров микроклимата - температуры воздуха и поверхностей, влажности и подвижности воздуха, концентрации газовых примесей. Современные измерители обладают возможностью автономного сохранения результатов измерений за длительный период и периодического считывания результатов с помощью дистанционного сканирования. Это позволяет размещать измерители во многих точках помещения.
Результаты измерений обрабатываются и хранятся в компъютере. Следует иметь в виду, что полномерное проведение мониторинга микроклимата зданий и сооружений достаточно дорогостоящее мероприятие.
Помимо натурных обследований, возможно воспроизведение процессов в лабораторных условиях на моделях, подобных натурному объекту. Лабораторно- модельный метод обладает рядом преимуществ перед методом исследований в натуре:
-возможностью изучения не выполненных еще в натуре объектов;
-возможностью систематического изучения влияния какого либо фактора, выделенного из всей совокупности влияющих на процесс факторов;
-возможностью изучения быстро протекающих явлений, неуловимых в натурных условиях.
Помимо этого моделирование оказывается дешевле натурных исследований.
При проведении эксперимента в натуре или на модели изучают конкретное явление и на основе обобщения результатов стремятся получить основания для расчета других родственных явлений.
Закономерно распространять результаты моделирования можно только на подобные явления. Применительно к моделированию процессов формирования микроклимата различают геометрическое, механическое и тепловое подобие.
Как известно из теории подобия, геометрическое подобие обусловлено равенством углов и пропорциональностью сходственных сторон в сравниваемых геометрических фигурах.
Под механическим подобием понимается пропорциональность скоростей и ускорений двух потоков, а также подобие сил, вызывающих подобные движения.
При тепловом подобии сохраняется подобие температуры и тепловых потоков
Данные опыта можно распространять на подобные явления, у которых выполняются условия однозначности и численно равны определяющие критерии подобия..
Условиями однозначности, подлежащими воспроизведению на модели являются:
-геометрическая форма моделируемого помещения;
-расположение и форма приточных и вытяжных отверстий в помещении;
-скорость движения и температура воздуха в приточных и вытяжных отверстиях;
-физические параметры воздуха (плотность, вязкость, теплоемкость, теплопроводность);
-источники и стоки тепла, влаги, паров и газов (расположение и форма, температура и концентрация, мощность).
Основными критериями механического подобия являются:
- Рейнольдса (Re), определяющий соотношение между инерционными силами и силами вязкости;
-Фруда (Fr), выражающий соотношение между гравитационными и инерционными силами;
-Архимеда (Ar), характеризующий соотношение сил инерции и вытеснения;
-Эйлера (Eu), определяющий соотношений сил давления и динамическими силами.
Тепловое подобие определяется следующими критериями:
-Прандтля (Pr),характеризующего физические свойства воздуха;
-Пекле тепловой (Pe), аналогичный критерию Рейнольдса;
-Нуссельта (Nu), характеризующий процесс теплообмена на границе между телом и жидкостью.
Во многих случаях выполнить все условия однозначности оказывается трудно. Здесь на помощь приходит замечательное свойство методологии моделирования, называемое автомодельностью. Область автомодельности - это такая область явления, в пределах которой не требуется соблюдения равенства отдельных критериев.
Наиболее распространенным явлением автомодельности, которым широко пользуются в моделировании аэродинамических и тепловых процессов, служит движение жидкости в зоне турбулентного течения. Это обстоятельство позволяет расширить возможности моделирования, заменив потокораспределение воздуха в натурных условиях потокораспределением воды. Условия подобия будут соблюдаться, если установлено, что течение в том и другом случае является развитым турбулентным. Проявлением этого условия обычно считают Re > 2320
Примером подобного случая может служить моделирование аэродинамических процессов в гидравлическом лотке (см.рис.2.4).В этом устройстве движущийся поток воздуха моделируется движущимся по рабочему столу плоским потоком воды. Если в потоке оказывается контур испытуемого предмета (например здания), то задача состоит в визуализации характера движения воды в зоне возмущения. Для визуализации обычно используют алюминиевую пудру, которая равномерно растекается по поверхности воды и не тонет.
При фотографировании модели на снимке четко видны все завихрения и линии тока воды, которые оставляют движущиеся частички пудры. Описанный прибор моделирует плоскую картину или двухмерный процесс обтекания, Известны исследования потокораспределения в трехмерном, объемном лотке. Например, таким образом проводилось исследование характера обтекания здания потоком воздуха.
Другим примером автомодельности служит процесс свободного движения жидкости, вызванного разной плотностью. Так, при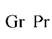 > 2 х 107 закономерность процесса не зависит от линейного размера и температуры источника, что удобно использовать при моделировании конвективных течений и струй, не заботясь о равенстве критерия Архимеда в натуре и на модели.
> 2 х 107 закономерность процесса не зависит от линейного размера и температуры источника, что удобно использовать при моделировании конвективных течений и струй, не заботясь о равенстве критерия Архимеда в натуре и на модели.
Пересчет полученных на модели результатов подразумевают использование масштабных соотношений. Наиболее понятным является масштаб длин, равный отношению размеров объекта в натуре и на модели
и на модели

Масштаб длин назначается произвольно, исходя из удобных для работы размеров модели. Помимо масштаба длин используются масштабы и других моделируемых величин: температуры, скорости, расхода воздуха и тепловых потоков и т.д..
Масштабные соотношения, за исключением масштаба длин, назначаются исходя из условия равенства определяющих критериев подобия. Это означает, что масштабы отдельных величин должны соотноситься так же, как соотносятся эти величины в критерии подобия. Поясним это обстоятельство, предварительно заметив, что масштаб площади равен квадрату, а масштаб объема - кубу масштаба длин. Рассмотрим соотношение масштабов для случая моделирования процессов в помещении с конвективным источником. Условие однозначности, помимо соблюдения геометрического подобия, состоит в равенстве критерия Архимеда в натуре и на модели .
.
Учитывая, что , получим соотношение масштабов в следующем
, получим соотношение масштабов в следующем
виде
где: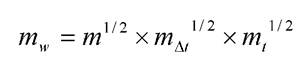
 -масштаб скорости;
-масштаб скорости;
 -масштаб разности температуры;
-масштаб разности температуры;
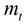 -масштаб температуры.
-масштаб температуры.
Аналогично можно вывести соотношение для других масштабов.
В качестве примера на рис.2.5 показана модель производственного помещения, расположенная в лаборатории и предназначенная для исследования процессов формирования микроклимата при различных вариантах систем вентиляции.