Законы алгебры логики

АЛ базируется на нескольких аксиомах, из которых выводят основные законы для преобразований с логическими переменными. Каждая аксиома представлена в двух видах, что вытекает из принципа дуальности логических операций, согласно которому операции конъюнкции и дизъюнкции допускают взаимную замену, если одновременно поменять 1 на 0, 0 на 1, знак Ú на ×, а знак × на Ú.

Аксиомы операции отрицания: , .

Аксиомы операций конъюнкции и дизъюнкции:

1а) 0×0=0 1б) 1Ú1=1

2а) 1×0=0×1=0 2б) 0Ú1=1Ú0=1

3а) 1×1=1 3б) 0Ú0=0

Законы АЛ вытекают из аксиом и также имеют две формы выражения а) и б).

1. Переместительный закон

а) a×b=b×a б) aÚb=bÚa

2. Сочетательный закон

а) a(bc)=(ab)c=abc б) aÚ(bÚc)=(aÚb)Úc=aÚbÚc

3. Закон тавтологии

а) a×a=a б) aÚa=a

4. Закон обращения: если a=b, то

5. Закон двойной инверсии: =a

6. Закон нулевого множества

а) a×0=0 б) aÚ0=a

7. Закон универсального множества

а) a×1=a б) aÚ1=1

8. Закон дополнительности

а) a×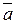=0 б) aÚ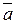=1

9. Распределительный закон

а) a(bÚc)=ab+a б) aÚ(bc)=(aÚb)( aÚc)

10. Закон поглощения

а) aÚab=a б) a(aÚb)=a

11. Закон склеивания

а) (aÚb)(aÚ)=a б) a.bÚ a.=a

12. Закон инверсии (закон Де Моргана)

а) 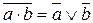б)

или после инвертирования

в) г)