Линейный конгруэнтный метод

 

Наилучшие из известных сегодня методов имитации случайных чисел представляют собой частные случаи схемы, предложенные в 1948 году Д.Х.Лемером.

Суть метода: Выбираем четыре "магических числа":

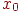– начальное значение,

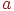– множитель,

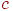– приращение,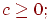

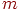– модуль,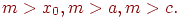

Тогда искомая последовательность случайных чисел получается из соотношения:

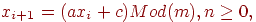
(7.1)

т. е. каждое случайное число – это остаток, при делении (ax_i+c) на m (операция Mod - "определение остатка", термин взят от слова "modulo" – в переводе "остаток").

Последовательность, полученная из соотношения (7.1) называется линейной конгруэнтной последовательностью.

Пример: x₀ = a = c = 7, m = 10.

Тогда последовательность имеет вид: 7, 6, 9, 0, 7, 6, 9, 0,…

Как видно, при выбранных значениях "магических чисел" последовательность почти сразу "зациклилась", длина периода = 4.

Из этого примера видно, что "магические числа" нельзя выбирать произвольно. Проведено много исследований и доказано теорем по вопросу "как правильно выбирать" "магические числа".

Метод получения случайных чисел при c=0 называется "мультипликативный конгруэнтный метод", при - "смешанный конгруэнтный метод". При c=0, выработка последовательностей происходит быстрее, но при этом уменьшается длина периода последовательностей.

Первоначально в методе Лемера было принято c=0. Идея получения более длинных последовательностей за счет принадлежит Томпсону и независимо Ротенбергу.

Выбор модуля m. Для получения длинных последовательностей и для увеличения скорости вычисления рекомендуется m выбирать равным размеру машинного слова. Для 32^х разрядного машинного слова m = 2³¹=2147483648, (левый нулевой бит слова отведен под знак числа).

При этом в 32^х разрядном машинном слове, максимальное целое число, размещающее в машинном слове, равно

Тогда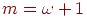

Значение множителя также влияет на длину периода последовательностей. По этому вопросу также проведено много исследований.

Линейные конгруэнтные последовательности – не единственный из предложенных источников случайных чисел. Его можно обобщить, превратив его, например, в квадратичный конгруэнтный метод

Известен квадратичный метод, предложенный Р. Ковэю:

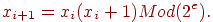
Известен метод получения случайных чисел, где реализуется последовательность Фибоначчи:

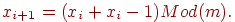
Известен также метод получения случайных чисел, предложенный Грином:

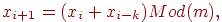
где k- большое число.

Имеются еще, так называемые, аддитивные методы, где не требуются операции умножения и деления, и другие методы.