Характеристическая функция коалиционной игры

Объединение игроков в коалицию К превращает их в одного игрока с множеством стратегий, получаемым объединением стратегий игроков, вошедших в коалицию. Очевидно, выигрыш коалиции К в ситуации Х равен

H^(K)(x) =— сумма выигрышей всех участников коалиции.

Деятельность игроков, не вошедших в коалицию, для гарантированного выигрыша можно рассматривать как помеху, т.к. интересы этого 2го игрока прямо противоположны интересам коалиции.

Таким образом осуществляется переход от коалиционной игры Г к игре Г^(К) — антагонистической игре коалиции против всех остальных (игра двух объединенных игроков с антагонистическими интересами).

Это рассуждение, в соответствии с принципом максимина, рассматривает выигрыш v(k), kI, 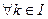; рассматриваются все коалиции, которые могут образоваться в игре.

Значение v(k), 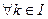— характеристическая функция коалиционной игры. Содержательно характеристическая функция может иметь разные происхождения.

ПРИМЕР. Пусть I — группа работников одинаковой квалификации, которые способны выполнить работу в а единиц (каждый). Тогда любая коалиция К с численностью игроков =|k| будет иметь выигрыш v(k)=|k|*a.

Участники коалиции — болваны, т.к. присоединяясь к коалиции они могут увеличить ее выигрыш только на величину, которую они способны заработать вне коалиции, действуя самостоятельно.

В общем случае присоединение j-ого игрока к коалиции может увеличить выигрыш каждого игрока, входящего в коалицию. В этом случае выигрыш i-ого игрока будет равен , где a_i — собственный выигрыш i-ого игрока, b_ij — выигрыш i-ого игрока от того, что в коалицию входит j-ый игрок.

 

Очевидно, если просуммировать выигрыш по всей коалиции, получим:

 

v(k)== ,

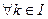
ПРИМЕР. Имеется рынок (например, автомобильный), где есть продавец (Пр) и два покупателя (П₁ и П₂). Продавец владеет товаром (неделимым) стоимостью а; первый покупатель (П₁) оценивает этот товар стоимостью b, второй (П₂) — стоимостью с:

Пр П₁ П₂

a b c

если a > max(b,c), игры не будет: продавец уйдет с рынка. Игра уместна, если, например, a<b<c.

Вначале полезности таковы: Пр П₁ П₂

a 0 0

Пусть первый покупатель (П₁) купил товар полезностью х, тогда полезности будут следующими: Пр П₁ П₂

х b-x 0

если П₂ купит товар за х,то: Пр П₁ П₂

х 0 с-х

Рассмотрим характеристическую функцию:

v(Пр)=a v()=0

v(П₁)=v(П₂)=v(П₁ П₂)=0

v(Пр,П₁)=b

v(Пр,П₂)=c

v(Пр,П₁,П₂)=с