Формулы структурной амплитуды для кристаллов с разными ячейками Бравэ

 

Если атомы жестко связаны в структуру, то это будет структурная амплитуда – амплитуда луча, рассеянного одной элементарной ячейкой.

Наличие элементов симметрии и непримитивность решетки кристалла обусловливают взаимосвязь координат отдельных атомов элементарной ячейки. Наиболее простую форму взаимосвязи дают центрированные решетки. Например, в объемноцентрированной решетке (- типа) все атомы связаны попарно: если координаты одного атома , то обязательно имеется другой атом того же сорта с координатами

 

(1).

 

Ранее была получена формула для расчета структурной амплитуды (рассеивающей способности) любого количества атомов:

 

, (2)

 

где , , . (3)

 

Формулу (2) запишем сначала с учетом (3), а потом (1)

 

. (4)

 

Рассчитаем для кристалла - типа:

В этом случае формула (2) примет вид

 

. (5)

Коэффициент, стоящий перед знаком , может иметь только два значения: 2 при , , и 0 при , 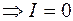. Следовательно, отличную от нуля интенсивность будут иметь только те отражения, индексы которых удовлетворяют соотношению , где 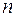- четное число.

Таким образом, мы получили правило погасания для объемноцентрированной ячейки. Аналогичным способом можно найти формулу структурной амплитуды для других случаев непримитивных решеток.

Этот пример показывает, что совсем не обязательно проводить суммирование по всем атомам элементарной ячейки. В зависимости от типа решетки и симметрии структуры верхний предел суммы может уменьшаться вдвое, вчетверо и т.д.