Лекция Температурный режим горного массива

 

Температурным полем называется совокупность значений температуры в данный момент времени во всех точках изучаемого пространства. Математическое выражение нестационарного температурного поля, когда температура каждой точки меняется с течением времени, имеет вид:

Т = f(x, y, z, t) (3.1)

Стационарное, т.е. не изменяющееся во времени температурное поле описывается зависимостью:

t = f(x, y, z); ¶T/¶t = 0.

Температурное поле можно охарактеризовать с помощью изотермических поверхностей. Изотермической поверхностью называется геометрическое место точек, имеющих в данный момент времени одинаковую температуру. Одна и та же точка среды не может одновременно иметь различную температуру, поэтому изотермические поверхности не пересекаются, а либо оканчиваются на поверхности тела, либо целиком располагаются внутри него. Пересечение изотермических поверхностей плоскостью дает на этой плоскости следы в виде семейства кривых, называемых изотермами.

Вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной от температуры по этому направлению, называется температурным градиентом

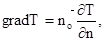(3.3)

где 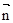– единичный вектор, нормальный к изотермической поверхности и направленный в сторону возрастания температуры.

Количество теплоты, передаваемое в единицу времени через изотермическую поверхность, называется тепловым потоком dQ.

Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности q = dQ/dF, называется плотностью теплового потока.

Перенос теплоты осуществляется тремя основными способами: теплопроводностью, конвекцией и тепловым излучением.

Теплопроводность – процесс переноса теплоты в сплошной среде микроструктурными элементами вещества, обусловленный переменностью температуру в рассматриваемом пространстве. Внутренний механизм явления теплопроводности подробно описан выше.

В основе переноса теплоты теплопроводностью лежит закон Ж.Фурье. который гласит: плотность теплового потока прямо пропорциональна температурному градиенту:

(3.4)

Конвекция – это процесс переноса теплоты при перемещении микроскопических частиц жидкости или газа в пространстве из области с одной температурой в область с другой. В этом случае перенос теплоты в среде неразрывно связан с переносом самой среды

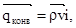(3.5)

т.е. в единицу времени через единицу контрольной поверхности нормально к ней проходит масса жидкости из области с одним значением энтальпии среды в область с другим значением и вместе с массой переносится энергия q_конв. Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно происходит соприкосновение частиц, имеющих различные температуры. В результате конвективный теплообмен описывают уравнением

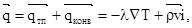(3.6)

где – вектор плотности молекулярного переноса (теплопроводность), обусловленный неоднородностью поля температуры; 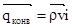– вектор плотность конвективного (молекулярного) переноса, обусловленный существованием движения среды.

Во многих случаях поток среды частично или полностью ограничен поверхностями твердых тел (стенками). Конвективный теплообмен между движущейся средой и поверхностью раздела называется конвективной теплоотдачей.

При расчетах теплоотдачи используют закон Ньютона-Рихмана:

dQ_c = a(T_пов – t_с)dF, (3.7)

где dQ_c – тепловой поток от жидкости к элементу поверхности; T_пос и t_с – соответственно температура поверхности тела и окружающей жидкой или газообразной среды.

Коэффициент теплоотдачи a учитывает конкретные условия процесса и представляет собой количество теплоты, передаваемое в единицу времени с единицы поверхности при разности температур твердого тела и среды один градус.

Роль коэффициента теплоотдачи a не аналогична роли, например, коэффициента теплопроводности l_п в законе Фурье. В то время как величина l_{п –} физический параметр среды (вещества). Коэффициент теплоотдачи a представляет собой сложную функцию тепловых и динамических процессов, развивающихся в непосредственной близости от поверхности теплообмена. Во всех случаях величина a определяется закономерностями развития у поверхности омываемого жидкостью твердого тела, т.н. гидродинамического и теплового пограничных слоев. Коэффициент теплоотдачи оказывается связанным с толщиной теплового пограничного слоя a = l_ж/d_тс, т.е. (где l_ж – теплопроводность жидкости).

Таким образом, коэффициент теплоотдачи представляет собой величину, обратную термическому сопротивлению (Р_тс = d_тс/l_ж) теплового пограничного слоя.

В свою очередь, значение d_тс зависит от закономерностей формирования теплового пограничного слоя и определяется природой возникновения движения среды.

Различают свободную и вынужденную конвекцию. Свободной конвекцией называется движение жидкости, вызванное неоднородным распределением массовых сил, в частности, обусловленное разностью плотности нагретых и холодных слоев, находящихся в поле тяготения. В этом случае нагретые слои, имеющие меньшую плотность, под действием архимедовой силы движутся вверх, и, наоборот, охлажденные слои движутся вниз.

Вынужденной конвекцией называется движение жидкости, вызванное действием внешних поверхностных сил, создаваемых работой насосов, вентиляторов, ветра и т.д. Вынужденное движение в общем случае может сопровождаться свободным движением. Доля и перенос теплоты свободной конвекцией тем больше, чем больше разница температур отдельных частей среды и чем меньше скорость вынужденного движения.

Численные значения коэффициента теплоотдачи a изменяются в широких пределах: при свободной конвекции воздуха – 5-25, воды – 20-100, при вынужденной конвекции воздуха – 10-200, воды – 50-10000, для кипящей воды – 3000-100000 Вт/(м²×К) .

Теплообменом излучением (лучистым теплообменом) называются процессы превращения внутренней энергии вещества в лучистую (в энергию фотонов или электромагнитных волн), распространения этой энергии в пространстве и поглощения ее другими телами с последующим превращением во внутреннюю энергию.

Тепловое излучение сосредоточено между длинами волн от 10^-3 до 0,7×10^-6 м. Большинство твердых и гладких тел имеет сплошной (непрерывный) спектр излучения, т.е. излучает энергию всех длин волн от 0 до ¥.

В основе большей части расчетных соотношений лучистого теплообмена, используемых в технике, лежит закон Стефана-Больцмана, в соответствии с которым количество теплоты в единицу времени (тепловой поток) излучением между телами определяется уравнением:

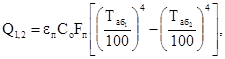(3.8)

где Т_аб1иТ_аб2 – абсолютная температура тел 1 и 2; F_{п –} приведенная поверхность излучения тел 1 и 2.

Температурное поле в вещественной среде, в которой процессы переноса теплоты осуществляются теплопроводностью и конвекцией, описывается с помощью дифференциальных уравнений непрерывности (сплошности), энергии и движения. В основе этих уравнений лежат законы сохранения массы, энергии и количества движения.

Уравнение непрерывности для несжимаемой среды r_ж = const имеет вид:

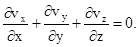(3.9)

Используя векторную форму записи, уравнение (3.9) можно записать в виде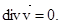

Уравнение энергии описывает температурное поле в изучаемой среде, получено в предположении, что среда несжимаема и однородна, а теплота, выделяющаяся в ней, равна Q (Вт):

(3.10)

Уравнение (3.10), введя обозначения оператора Лапласа и субстанциональной производной , можно записать в более компактной форме:

¶Т/¶t = Ѳ + Q/cr (3.11)

Если в изучаемой среде отсутствует конвективный перенос, то уравнение энергии переходит в уравнение теплопроводности

¶Т/¶t = аÑ²Т + Q/cr (3.12)

При стационарных процессах (¶Т/¶t = 0) и отсутствии выделения или поглощения теплоты (Q = 0) уравнение (3.12) принимает вид и называется уравнением Лапласа

Ñ²Т = 0. (3.13)

Условия однозначности. Дифференциальные уравнения описывают бесчисленное множество конкретных процессов. Чтобы выделить рассматриваемый процесс и однозначно определить его, к системе дифференциальных уравнений присоединяются условия однозначности, которые дают математическое описание всех частных особенностей рассматриваемого явления. Условия однозначности состоят из:

1) геометрических условий, характеризующих форму и размеры тела или системы, в которой протекает процесс;

2) физических условий, характеризующих физические свойства среды;

3) временных или начальных условий, характеризующих особенности процесса в начальный момент времени;

4) граничных условий, определяющих особенности протекания процесса на границах жидкой или твердой среды.

Задание начальных условий заключается в том, что для некоторого момента времени t = t_о (обычно полагают t_о = 0) должны быть известных функции пространственных координат T(x, y, z, t_o) = f₁(x, y, z); 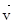(x, y, z, t_o) = (x, y, z). В простейшем случае начальные условия имеют вид:

f₁(x, y, z) = T_o;

f₂(x, y, z) = ; (3.14)

f₃(x, y, z) = P_o.

что соответствует независимости начального распределения полей скорости, давления и температуры от пространственных координат.

В качестве граничных условий для скорости движения жидкостей (уравнения движения) могут быть заданы распределения скоростей жидкости на входе в систему, на большом удалении от рассматриваемой поверхности теплообмена и т.п.

В уравнении энергии (теплопроводности) для искомой функции температуры могут быть заданы следующие граничные условия.

1. Граничные условия первого рода, когда на поверхности, ограничивающей исследуемую область, задано распределение температур как функция координат и времени:

T_пов = j(x, y, z, t). (3.15)

В горно-теплофизических расчетах граничные условия первого рода могут быть использованы при постановке задач, описывающих температурные поля в породах, окружающих горные выработки, при интенсивном испарении влаги с поверхности пород при движении теплоносителя по скважинам или геотермальному коллектору в системах извлечения геотермальной энергии и т.п.

2. Граничные условия второго рода, когда на поверхности в функции координат и времени задана плотность теплового потока, т.е. производная от температуры по нормали к поверхности:

(3.16)

Возможен случай задания однородного граничного условия второго рода

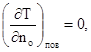(3.17)

т.е. условия отсутствия потока теплоты на поверхности тела, так называемая тепловая изоляция. Такое условие часто задается при равномерном обогреве поверхности тела, имеющего геометрическую симметрию. Например, задача симметричного прогрева пластины толщиной 2R(½х½ < R), являющаяся, например, физической моделью для исследования формирования температурных полей в ленточном целике, когда на ограничивающих поверхностях х = ±R с помощью инфракрасных излучателей задана плотность тепловых потоков q₁ = q₂ = q_о) сводится к эквивалентной задаче: заданы тепловой поток q_о на поверхности х = R и условие (3.7), т.е. q = 0, в центре симметрии пластины х = 0. Другой пример задания условия второго рода относится к формированию в горном массиве заданного температурного распределения с помощью установленной в выработке холодильной машины. Плотность теплового потока при этом равна отношению тепловой мощности холодильной машины Q(t) к поверхности выработки F, т.е. q = Q(t)/F.

3. Граничные условия третьего рода, в которых тепловой поток предполагается пропорциональным разности температуры поверхности твердого тела, описываемого жидкостью Т_пов., и температуры жидкости t:

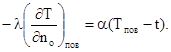(3.18)

Граничное условие третьего рода широко применяется в горной теплофизике для исследования температурных полей в системе горный массив – воздушная струя, а также при фильтрации газа и жидкости в пористых средах.

4. Граничные условия четвертого рода сводятся к одновременному заданию равенства температур и тепловых потоков на границе раздела x, когда решается задача о теплообмене двух сред с температурами Т₁(x, y, z, t), T₂(x, y, z, t), например, твердое тело – жидкость, твердое тело – твердое тело, жидкость – жидкость), в каждой из которых перенос теплоты описывается своим уравнением энергии:

Т₁ = Т₂; (3.19)

(3.20)

Равенство (3.19) выражает условие непрерывности температурного поля, а равенство (3.20) – закон сохранения энергии на поверхности соприкосновения двух сред (или тел). Условия (3.19), (3.20) называются еще условиями идеального теплового контакта, а также неуправляемыми граничными условиями в отличие от граничных условий первого – третьего родов (управляемые граничные условия).

В задачах горной теплофизики граничные условия четвертого рода в основном используются при вычислении температурных полей в неоднородных по теплофизическим свойствам породных массивах, находящихся в контакте друг с другом, например, бетонная закладка – руда, гидравлическая закладка – уголь, бетонная крепь – горный массив.

Таким образом, при конвективном теплообмене твердого тела с жидкостью в случае стационарного температурного поля (¶Т/¶t = 0) целесообразно использовать граничные условия третьего рода – соотношение (3.18), а в случае нестационарного поля (¶Т/¶t ¹ 0) при точной формулировке задачи необходимо применять граничные условия четвертого рода (3.19), (3.20). В случае нестационарного лучистого теплообмена при большой разности температур поверхности и среды необходимо применять граничные условия второго рода (соотношение (3.16)). При малой разнице температур, когда [T_пов(t) – t(t)] ® 0, можно использовать закон Ньютона, т.е. граничные условия третьего рода.

Особый интерес представляет задание граничных условий на поверхностном соприкосновении двух тел, где происходит агрегатный переход вещества (например, вода – лед, или лед – вода, твердая порода – расплав, или расплав – твердая порода). Температурные поля в каждом из этих тел описываются уравнениями энергии типа (3.11) или (3.12), а соотношение (3.20) на границе раздела заменяется так называемым граничным условием Стефана:

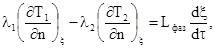(3.21)

где L_фаз – теплота агрегатного перехода, Дж/кг.

В качестве примера использования вышеприведенных уравнений осуществим расчет геотемпературного поля. Особенности его формирования определяются взаимодействием внутренних и внешних источников и стоков теплоты. Внутренние источники являются относительно стабильными (радиоактивный распад, гравитационная дифференциация и пр.), и с их действием связано повышение температуры пород с глубиной. Основной внешний источник – переменная во времени солнечная радиация, вызывающая периодические температурные колебания горного массива, затухающие на определенной глубине от поверхности Н_гтз, называемой глубиной гелиотермозоны или глубиной нейтрального слоя.

Нормальное геотемпературное поле верхних участков земной коры характеризуется сравнительно быстрым ростом температуры пород с глубиной Н. На его общем фоне происходят связанные со строением массива пород, рельефом поверхности Земли, гидрогеологическими условиями и другими факторами, изменения, определяющие вариации и аномалии геотемпературного поля.

Температурный режим поверхности Земли в конкретном районе характеризуется переменной во времени температурой поверхности почвы Т, связанной с температурой атмосферного воздуха в данном районе t:

T = T_ср + А_Тsin2pt/t_max, (3.22)

где Т_ср – среднегодовая температура почвы, °С, Т_ср, = t_ср + 2; t_ср – среднегодовая температура воздуха °С, t_ср; A_T » A_t – 2,5; А_Т и А_t – амплитуда колебаний температуры почвы и воздуха на поверхности Земли °С, t – время от начала перехода температуры воздуха через среднегодовое значение в весенний период (апрель) до текущего момента; t_{max –} продолжительность года, ч, t_max = 8760 ч.

Соотношение (3.22) представляет собой граничное условие (I рода) к уравнению (3.12), которое для рассматриваемого случая принимает вид (поверхность Земли считается плоской, горный массив моделируется полуограниченным телом, координата х отсчитывается от поверхности вглубь Земли).

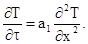(3.23)

Начальным условием к уравнению (3.23) является равенство температуры пород Т(х, t) среднегодовой температуры почвы Т_ср, а дополнительное граничное условие формулируется как отсутствие изменения температурного поля на некоторой глубине Н, т.е. Т₁(х, Н) ® Т_ср.

Решение этого уравнения при данных начальных и граничных условиях дает возможность приближенно оценить динамику температуры пород в пределах гелиотермозоны:

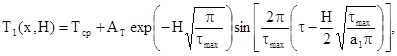(3.24)

Используя формулу (3.24), несложно вычислить глубину гелиотермозоны Н_гтз. Для этого примем, что амплитуда колебаний температуры на глубине Н_гтз не превышает 0,1°С, т.е. А_тн = 0,1. Тогда получим:

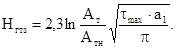(3.25)

Верхние слои почвы в зимний период при отрицательной температуре атмосферного воздуха и поверхности Земли будут промерзать, а в летний период наоборот оттаивать. Для определения глубины промерзания пород необходимо уравнение (3.23), которое будет описывать, например, распределение температур в мерзлой зоне, дополнить уравнением, характеризующим температурное поле в еще не промерзшем грунте [Т₂(х, t)]:

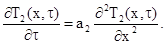(3.26)

Граничным условием к уравнению (3.25) будет равенство температуры поверхности Земли среднезимней температуре Т₁(0, t) = Т₃. На глубине промерзания грунта х = x_о выполняется граничное условие Стефана

Т₁(x_о,t) = Т₂(x_о,t) = Т_фаз; (3.27)

(3.28)

где l₁, l_{2 –} соответственно теплопроводности мерзлого и талого грунта Вт/(м×°С); r₂ – плотность талых пород, кг/м³; L_ф – теплота агрегатного перехода воды в лед (L_ф = 335,2 кДж/кг); w – весовая влажность (льдистость) грунта, доли ед.; Т_фаз – температура фазового перехода, °С.

Дополнительным граничным условием к уравнению (3.26) является равенство нулю теплового потока на некоторой глубине Н_о от поверхности Земли, т.е. ¶Т₂(х, t)/¶х½_х=Но ® 0 (или неизменность температурного поля на этой глубине Т₂(Н_о, t) = Т_ср).

Решение задачи о промерзании почвы, выполненное еще в XIX веке Стефаном, имеет следующий вид:

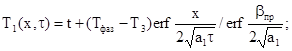(3.29)

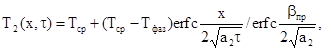(3.30)

где - интегралы вероятности.

Коэффициент b_пр, характеризующий скорость углубления зоны промерзания, определяется из трансцендентного уравнения:

(3.31)

В свою очередь, глубина зоны промерзания составляет:

(3.32)

Тепловой поток, отводимый от промерзающих пород в окружающую среду, будет равен:

(3.33)

Уменьшение глубины промерзания пород достигается за счет нанесения на поверхность теплоизоляционного покрытия заданной толщины d_из и теплопроводности l_из. При этом соотношение теплопроводности к толщине теплоизоляционного покрытия должно удовлетворять равенству:

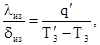(3.34)

где Т'₃ – температура поверхности Земли после нанесения теплоизоляционного покрытия, °С.

При глубине расположения пород, превышающей глубину нейтрального слоя, температурное поле Земли может считаться не зависящим от времени, что позволяет использовать для расчетов температурного распределения уравнение (3.4). Особенности формирования температурного поля на этих глубинах определяются лишь геологическими и геотермическими условиями рассматриваемого района: типом и мощностью различных слоев пород, их теплопроводностью, тепловым потоком. Так как тепловой поток связан с температурным градиентом соотношением (3.4), то значение температуры пород на нижней границе i-го слоя породы будет составлять:

Т_Нi = Т_Вi +g_Гi(H_i – H_i-1), (3.35)

где Н_i, Н_i-1 – глубины расположения верхней и нижней границ i-го слоя пород, м; Т_Вi – температура пород на верхней границе слоя, °С; g_Гi – геотермический градиент в i-ом слое, равный отношению теплового потока к коэффициенту теплопроводности l_i:

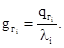(3.36)

Средняя плотность глубинного теплового потока на поверхности Земли составляет 0,072 Вт/м². Расчет по формуле (3.35) начинается со значений Т_Bi и Н_i-1, соответствующим температуре и глубине нейтрального слоя.

В качестве другого примера рассмотрим расчет температурных полей в горном массиве, окружающем выработки.

Математическая формулировка задачи будет зависеть от геометрической формы выработки и типа граничного условия на контакте воздушного потока с породами. Геометрическая форма выработок выбирается в зависимости от соотношения их длины l_выр, ширины b_выр и высоты h_выр следующим образом (рис. 3.1):

а) при b_выр/h_выр > 2 – поперечное сечение выработки принимается щелеобразным, а сам горный массив, окружающий выработку моделируется полуограниченным пространством;

б) при l_выр/b_выр > 2 и b_выр/h_выр £ 2 – поперечное сечение выработки принимается круговым, а сама выработка – цилиндрической формы.

Выбор граничных условий зависит от величины коэффициента теплоотдачи a. при a £ 50 Вт/м²×°С теплообмен между воздухом и породами описывается граничными условиями III-го рода, а при a > 50 Вт/м^{2 –} граничными условиями I-го рода.

Типичная математическая постановка задачи от теплообмене воздушного потока с горным массивом, окружающем цилиндрическую выработку кругового поперечного сечения, при допущениях независимости теплофизических свойств пород от температуры и времени, а также пренебрежимо малыми величинами тепловых потоков в породах и в воздухе вдоль оси выработки соответственно по сравнению с его радиальной составляющей и конвективным переносом, имеет вид:

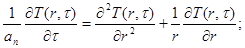(3.37)

T(r, 0) = Т_о; (3.38)

(3.39)

(3.40)

где R_ж – эквивалентный радиус выработки, м;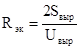; S_выр, U_выр – соответственно сечение и периметр выработки; Т_о – начальная температура пород, °С.

Решение системы уравнений (3.37) – (3.40) может быть осуществлено как строгими, так и приближенными аналитическими методами. При использовании последних распределение температуры пород дается зависимостью:

(3.41)

где d – так называемый радиус теплового влияния, зависящий от числа Фурье, связанного с временем теплообмена (Fо=a_пt/R_эк²), Bi – число Био 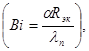R = r/R_эк.

Величина коэффициента теплоотдачи a определяется в зависимости от скорости движения воздуха v_в, геометрических параметров выработки и состояния ее поверхности, омываемой воздухом, которое учитывается коэффициентом шероховатости e_ш.

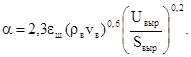(3.42)

Величина e_ш изменяется от 1 до 3,5.

В том случае, если в процессе формирования температурного поля в породах, окружающих выработку, происходят агрегатные переходы, то математическая формулировка задачи аналогична постановке, характеризующей процесс промерзания поверхностного слоя Земли.