Теорема Пуансо (о приведении системы сил к заданному центру)

Теорема. Любая система сил эквивалентна системе, состоящей из силы и пары сил. Сила приложена в любой наперед заданной точке (центре приведения) и геометрически равна главному вектору системы сил. Момент пары равен главному моменту исходной системы сил относительно центра приведения.

Доказательство.

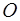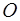Пусть точка – центр приведения (полюс приведения). Приведем исходную систему сил к центру , пользуясь леммой о параллельном переносе силы.

Вначале приведем силу к заданному центру (рис. 41), которая будет эквивалентна силе и паре :

, .

Аналогично поступим с остальными силами исходной системы (рис. 42).

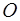Получим, что система ~ и парам , ,…,. Силы приложены в точке (сходящиеся силы) и могут быть заменены одной силой, приложенной в точке 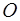и геометрически равной главному вектору

.

Система пар , ,…,по теореме о "сложении" пар эквивалентна одной паре , момент которой равен сумме моментов всех пар системы, которая в свою очередь равна главному моменту исходной системы сил относительно центра приведения

.

Теорема доказана.