Описание кругового движения векторным способом в общем случае
Обозначим  орт радиус-вектора
орт радиус-вектора  точки
точки 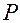 относительно точки отсчета
относительно точки отсчета  .
.
Согласно определению 2, на круговом движении должно выполняться
 , (1.3.4)
, (1.3.4)
 ,
,  ,
,  . (1.3.5)
. (1.3.5)
Тождества (1.3.5) справедливы для всех значений 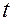 из промежутка времени, в течение которого совершается движение.
из промежутка времени, в течение которого совершается движение.
В общем случае при движении точки орт  меняет свое направление с изменением времени.
меняет свое направление с изменением времени.
Задавая такой закон  изменения направления орта
изменения направления орта  , при котором выполняются тождества (1.3.5), и, подставляя его в (1.3.4), придем к векторному способу задания кругового движения точки.
, при котором выполняются тождества (1.3.5), и, подставляя его в (1.3.4), придем к векторному способу задания кругового движения точки.
В частности, как и при координатном способе (см. п.2º), направление орта  можно задавать не в прямой зависимости от времени
можно задавать не в прямой зависимости от времени 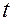 , а, например, через закон изменения угла
, а, например, через закон изменения угла  поворота, который совершает радиус-вектор точки
поворота, который совершает радиус-вектор точки 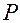 относительно некоторого фиксированного положения
относительно некоторого фиксированного положения  этой точки (см. рис.1.3.1).
этой точки (см. рис.1.3.1).