Пример применения алгоритма

 

Применение алгоритма рассмотрим на примере вычисления радиуса кривизны эллипса в любой его точке.

 

1. Уравнение эллипса в декартовых координатах имеет вид:

.

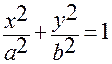2. Переходим к параметрическому уравнению эллипса:

, .

3. Задаем закон движения по эллипсу:

.

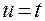4. Строим расчетные формулы для вычисления кинематических характеристик движения.

 

4.1). Формулы для скорости:

,

, (1.2.21)

.

4.2). Формулы для ускорения:

 

,

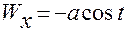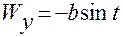, (1.2.22)

.

 

4.3). Формула для производной :

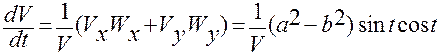. (1.2.23)

4.4). Формула для расчета радиуса кривизны в любой точке эллипса:

.

 

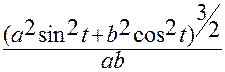Эта формула получена подстановкой в (1.2.17)

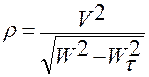(1.2.17)

величин , и , вычисленных по формулам (1.2.21), (1.2.22) и (1.2.23).

В декартовых координатах она будет иметь вид

 

. (1.2.24)

В частности, если , то эллипс вырождается в окружность.

 

Тогда

,

 

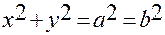и из (1.2.24) получим

в любой точке окружности.

 

Пусть . Вычисляем 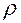в вершинах эллипса.

 

В вершинах на оси имеем 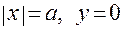. Для них из (1.2.24) получим

.

 

В вершинах на оси имеем . Из (1.2.24) следует, что в них

.