Проекции скоростей двух точек свободного твердого тела на прямую, проходящую через эти точки, равны, между собой.
Согласно равенству (6.20) имеем
,
но вектор 
перпендикулярен вектору 
; следовательно, 
и 
. Определим ускорения точек свободного твердого тела. Для этого продифференцируем по времени равенство (6.20):
. (6.21)
Замечая, что 
, 
– угловое ускорение тела в подвижной системе координат Aх2y2z2, а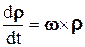 
, получим
Используя (6. 17), можно записать
.
где 
– вектор, имеющий начало в точке В, а конец в основании перпендикуляра, опущенного из В на 
(рис. 6.7).
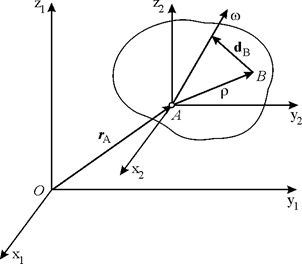Рис. 6.7.
| В окончательном виде ускорение точки свободного тела выражается следующим образом:
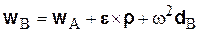 . (6.22)
Два последних члена дают ускорение точки В в ее движении вокруг полюса.
Таким образом, ускорение точки свободного тела равно
|