Механические свойства пассивной мышцы.

Под действием внешней нагрузки мышца деформируется (растягивается) и в ней возникают упругие силы ,стремящиеся вернуть мышцу в исходное состояние .При этом работа ,затраченная на деформацию , переходит в ‘энергию упругой деформации. С ростом деформации растут

 

и упругие силы. При равенстве величины упругой силы внешней нагрузке деформация останавливается . Следовательно, каждой длине мышцы ( степени ее деформации) отвечает соответствующее напряжение. .Увеличить напряжение невозбужденной мышцы можно только увеличивая ее нагрузку.

В качестве примера на рис 4 приведена обобщенная кривая « длина – напряжение « ; . н а рис 10 - аналогичные кривые ,полученные на трехглавой мышце плеча человека .

Зависимость между длиной мышцы и деформирующей ее силой была изучена еще Вебером в 1846 году. Им было показано, что по мере деформации мышцы одинаковая прибавка растягивающего мышцу груза вызывает все меньшее приращение ее длины. Форма кривой близка к гиперболе В определенном диапазоне длин эта связь лучше выражается уравнением экспоненты: логарифм напряжения линейно растет с ростом длины. При растягивании пассивной мышцы ее упругое напряжение прогрессивно возрастает в пределах растяжения до двух раз от равновесной длинны. Большинство мышц при максимальном суставном угле имеет длину , которая примерно на 20% больше равновесной, что отвечает максимальной силе тяги мышцы в условиях ее натуральной иннервации

Следует учитывать ,что сопротивление деформации во время растяжения оказывают преимущественно структурные элементы , входящие в ПарУК

 

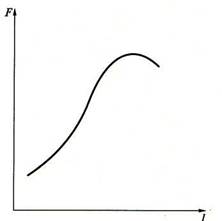
Рис. 4 Зависимость силы, разви­ваемой мышцей, от ее длины