Приведение масс

Приведение масс рассмотрим на примере механизма (рис.3,а).

Заменим заданный механизм его динамической моделью (рис.3,б). – сосредоточим в ней инертность всех звеньев механизма. Обозначим момент инерции модели . Следовательно, является эквивалентом инертности всего механизма и называется его приведенным моментом инерции. Величина определяется из условия равенства кинетических энергий модели и всего механизма :

. (8.9)

Рис.8.3

Кинетическая энергия модели определяется по формуле:

 

. (8.10)

Кинетическая энергия звена в общем виде может записана так:

, (8.11)

где 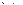- скорость центра масс звена ; 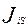- момент инерции звена относительно оси, проходящей через центр масс . В случае поступательного движения 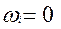. В случае вращательного движения вокруг оси уравнение (11) приводится к виду

.

Кинетическая энергия заданного механизма (рис.3,а) складывается из кинетических энергий его подвижных звеньев: . Звено 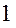участвует во вращательном движении, звено - в плоском, звено - в поступательном, звено - во вращательном. Поэтому

Подставив выражения и в исходное уравнение (9) и учитывая уравнение (4), получим

(8.12)

Практическое использование уравнения (12) может быть осуществлено или графически (с помощью планов возможных скоростей), или аналитически (с помощью аналогов скоростей).