Дисперсия альтернативного признака

Особый интерес представляет нахождение дисперсии альтернативного признака, т.е. признака, которым единицы изучаемой совокупности могут либо обладать, либо не обладать. В таких случаях наличие признака обозначается единицей, а его отсутствие - нулем. Доля единиц, обладающих интересующим нас признаком, обозначается через р, доля остальных единиц : q=1-p.

Определим для этих значений среднее значение альтернативного признака и его дисперсию.

Среднее значение альтернативного признака

так как p+q=1.

Дисперсия альтернативного признака

Подставив в формулу дисперсии q = 1- p получим:

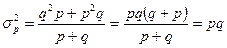
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих данным признаком.

Среднее квадратическое отклонение альтернативного признака

.