Символы взаиморасположения геометрических объектов и логических операций
| Обозначение | Смысловое значение | Пример символической записи |
| ( … ) | способ задания геометрического объекта в пространстве и на комплексном чертеже | А(А1, А2) – точка А задана на комплексном чертеже горизонтальной и фронтальной проекциями; S (А, b) – плоскость S задана прямой b и точкой А. |
| Î Ì , É | принадлежность | АÎl – точка А принадлежит прямой l; lÌS – прямая l лежит в плоскости S |
| º | совпадение | А1ºВ1 – горизонтальные проекции точек А и В совпадают. |
| // | параллельность | a // b – прямые a и b параллельны. |
| ^ | перпендикулярность | c^d – прямые c и d перпендикулярны. |
| _·_ | скрещивание | m _·_ n – прямые m и n скрещивающиеся. |
| Ç | пересечение | k Ç l – прямые k и l пересекаются. |
| `Ç | касание | l`Ç F =N – прямая l касается плоскости F в точке N. |
| È | объединение | АВ ÈВС ÈCD – ломаная линия ABCD. |
| ~ | подобие | DАВС ~ DDEF – треугольники ABC и DEF подобны. |
| @ | конгруэнтность | DАВС @ DDEF – треугольники ABC и DEF конгруэнтны, т.е. они могут быть совмещены в пространстве движением первого порядка. |
| = | равенство | /АВ/ = /CD/ – отрезки АВ и CD равны. |
| / | отрицание | А Ï l – точка А не принадлежит прямой l. |
| Ù | конъюнкция предложений (соответствует союзу «и») | K Î a Ù K Î d – точка K принадлежит прямым a и d. |
| Ú | дизъюнкция предложений (соответствует союзу «или») | А Î S Ú A Ï S – точка А принадлежит плоскости S или точка А не принадлежит плоскости S. |
| Þ Ü | логическое следствие – импликация (следовательно, поэтому) | a // b Ù c // b Þ a // c – прямые а и с параллельны прямой b, следовательно, они параллельны между собой. |
Продолжение таблицы 1
| Обозначение | Смысловое значение | Пример символической записи |
| Û | логическая эквивалентность (что то же самое) | A Î l Û A1 Î l1, A2 Î l2 – точка А принадлежит прямой l, следовательно, ее проекции лежат на одноименных проекциях прямой; справедливо и обратное утверждение: проекции точки А лежат на одноименных проекциях прямой l, следовательно, точка принадлежит этой прямой. |
| ® ¬ | отображение, преобразование |  – система ортогональных плоскостей  преобразуется в систему плоскостей  .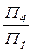
|
Таблица 2