ЛЕКЦИЯ 9: Показатели вариации в статистике

 

Информация о средних уровнях исследуемых показателей обыч­но бывает недостаточной для глубокого анализа изучаемого про­цесса или явления. Поэтому необходимо учитывать и вариацию значений отдельных единиц относительно средней, которая явля­ется важной характеристикой изучаемой совокупности. Значитель­ной вариации подвержены курсы акций, объемы спроса и предло­жения, процентные ставки в разные периоды времени.

Основными показателями, характеризующими вариацию, явля­ются размах, дисперсия, среднее квадратическое отклонение и ко­эффициент вариации.

Простейшим показателем, уже использованным выше при груп­пировке данных, является размах вариации. Он представляет собой разность максимального и минимального значений признака:

К = х_max - х_min.

Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеба­ние внутри этих границ. Этого недостатка лишена дисперсия, рас­считываемая как средний квадрат отклонений значений признака от их средней величины. Как и средняя величина, дисперсия может рассчитываться по-разному. Здесь перед нами невзвешенная фор­мула:

 

 

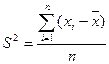
Если варианты значений изучаемого признака повторяются используется следующая формула:

 

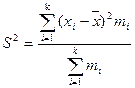
Наиболее широко используется для оценки вариации среднеквадратичное отклонение. Оно определяется как квадратичный корень из дисперсии и рассчитывается по формуле:

 

 

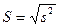
Рассмотренные показатели позволяют получить абсолютные значения вариации. Т.е. оценивать ее в единицах измерения исследуемого признака.

В отличии от них, коэффициент вариации измеряет относительную колеблемость (относительно среднего уровня) признака.

 

 

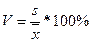
Показатели вариации повышают свою значимость если их использовать для целей сравнительного анализа. Можно сравнить показатели вариации разных совокупностей или показатели, взятые за разные периоды.

Показатели вариации являются составной частью или служат основой для расчета других статистических показателей.