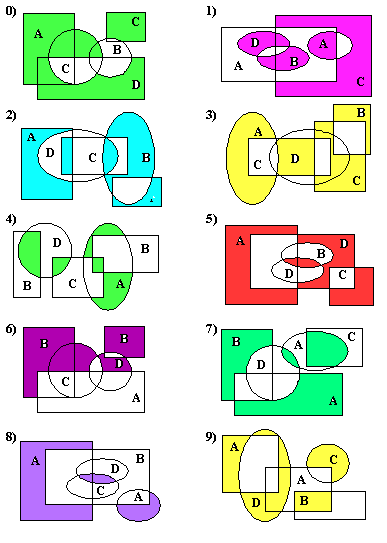
Представьте заштрихованные области формулами теории множеств


3. Упростите выражения:
0)X ∪ Y ∪ (X ∪ Y) ∩ Z º
 | ( | (  | Y) º
( | Y) º
(  D Z) ∩ (X ∩Y) º D Z) ∩ (X ∩Y) º
 | ( | (  | |  ) ∩ X º
(X ∪ Y) D (X ∩ ) ∩ X º
(X ∪ Y) D (X ∩  ∩ ∩  ) º ) º
| 1)  ∪ ∪  ∪ ∪  º
(X ∪ Y | Z) | (X ∩ Z) º
(X ∪ Y) ∩ (X D º
(X ∪ Y | Z) | (X ∩ Z) º
(X ∪ Y) ∩ (X D  ) º ) º
 D D  º º
 º º
|
2) 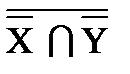 ∪ ∪  ∪ X º ∪ X º
 ∩ (Y | X ∪ Y) º
( ∩ (Y | X ∪ Y) º
(  ∩ ∩  ) D X º
( ) D X º
(  D D  ) | ) |  ∪ ∪  º
(X ∪Y) | (X ∩ (Z | Y)) º º
(X ∪Y) | (X ∩ (Z | Y)) º
| 3)(X ∩Y) ∪ (X ∩ 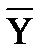 ) º ) º
 º
( º
(  D Z) ∪ (X ∩Y) º
X | ( D Z) ∪ (X ∩Y) º
X | (  ∩ (X ∪ ∩ (X ∪  )) º
( )) º
(  D X) | D X) |  º º
|
4)X ∩ Y ∪ (  ∪ ∪  ) º
X ∪Y | (X ∪ Y | ) º
X ∪Y | (X ∪ Y |  ) º
Y ∩ (X D Y) º
( ) º
Y ∩ (X D Y) º
(  ∪ ∪  ) D ) D  º º
 | ( | (  | |  ) º ) º
| 5) 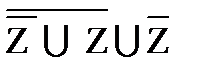 º
Z | ((X ∪ Y) ∪ Z) º º
Z | ((X ∪ Y) ∪ Z) º
 ∩ ( ∩ (  D D  ) º
(X | Z) ∪ (X ∩ Z) º
(X ∪ Y) ∪ (X D Y) º ) º
(X | Z) ∪ (X ∩ Z) º
(X ∪ Y) ∪ (X D Y) º
|
6)( X ∩ Y ) ∩ (X ∪ Z ) º
(X ∩ Y ∪ Z ) | X º
(  ) D ( ) D (  | Y) º
( | Y) º
(  D D  ) ∪ ) ∪  º º
 D D  º º  | |  º º
| 7)  ∪ X ∪ ∪ X ∪  º
X | (Y ∩ (X ∪ º
X | (Y ∩ (X ∪ 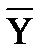 )) º
(Y D X) | )) º
(Y D X) |  º
( º
(  ∩ ∩  ) D (X ∪ Y) º
( ) D (X ∪ Y) º
(  D D  ) ∩( ) ∩(  | |  ) º ) º
|
8)X ∪ Y ∪  ∩ ∩  º
((X ∪ Y) | X) ∩ (Z | Y) º
Y D ( º
((X ∪ Y) | X) ∩ (Z | Y) º
Y D (  ∪ ∪  ) º ) º
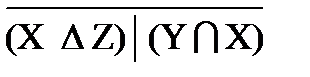 º
( º
(  ∩ ∩  ∩ Y) | (X ∪ Y) º ∩ Y) | (X ∪ Y) º
| 9)  ∪ ∪  ∪ (X ∪ Z ∩Y) º
X | (Y | ∪ (X ∪ Z ∩Y) º
X | (Y |  ) º
(X ∪ Y ∪ Z) D (X ∩Y) º ) º
(X ∪ Y ∪ Z) D (X ∩Y) º
 D ( D ( 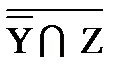 | Y) º | Y) º
 | (Z | Y) º | (Z | Y) º
|
Представьте заштрихованные области формулами теории множеств, упрощая, если возможно.