Формула полной вероятности и формула Байеса.

 

Выведем теперь еще две важные формулы – формулу полной вероятности и формулу Байеса.

Рассмотрим следующую задачу. Пусть требуется найти вероятность события А, которое происходит обязательно вместе с одним из событий 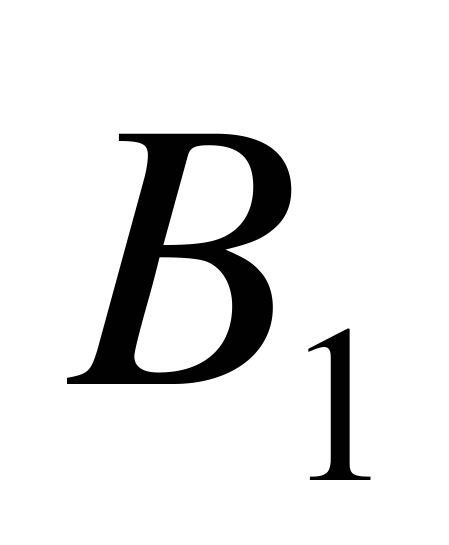, , 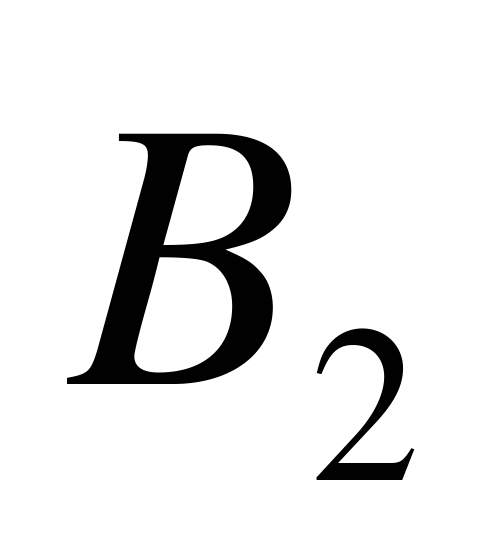… , 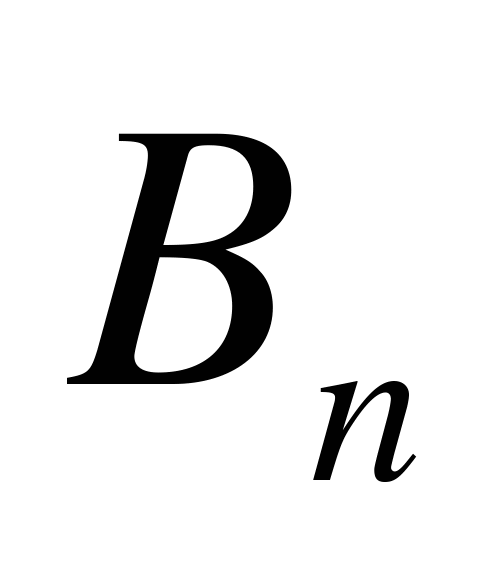образующих полную группу попарно несовместных событий. Тогда, если событие А наступило, то обязательно произошло одно из событий 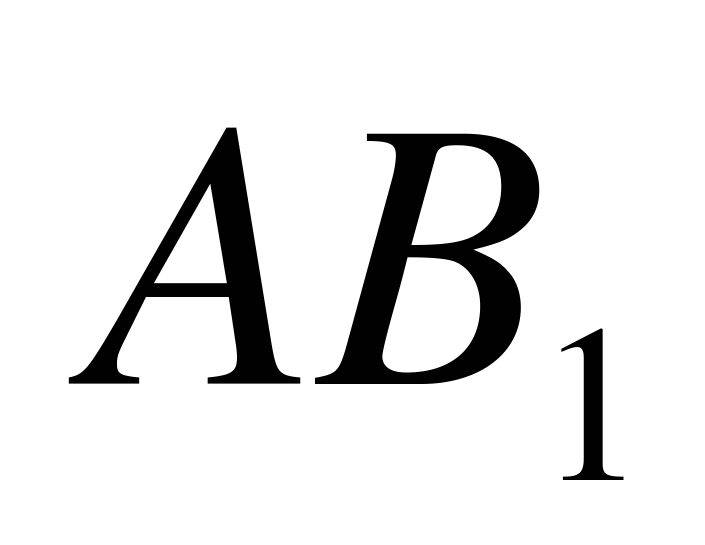, , 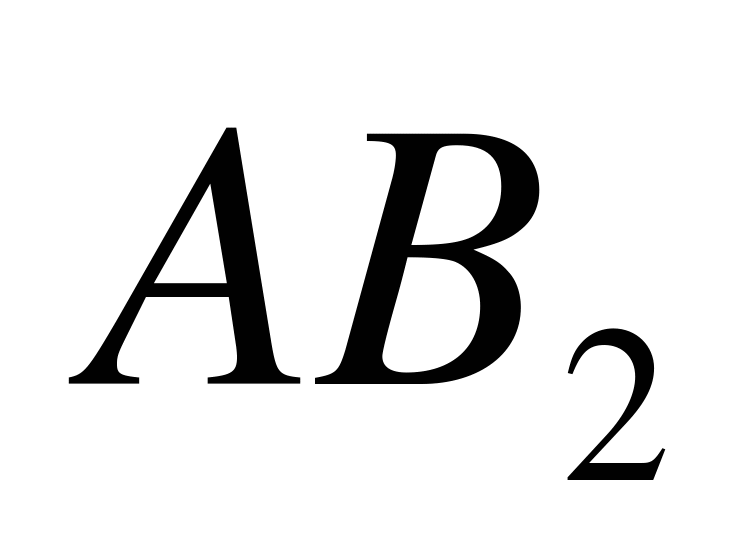… 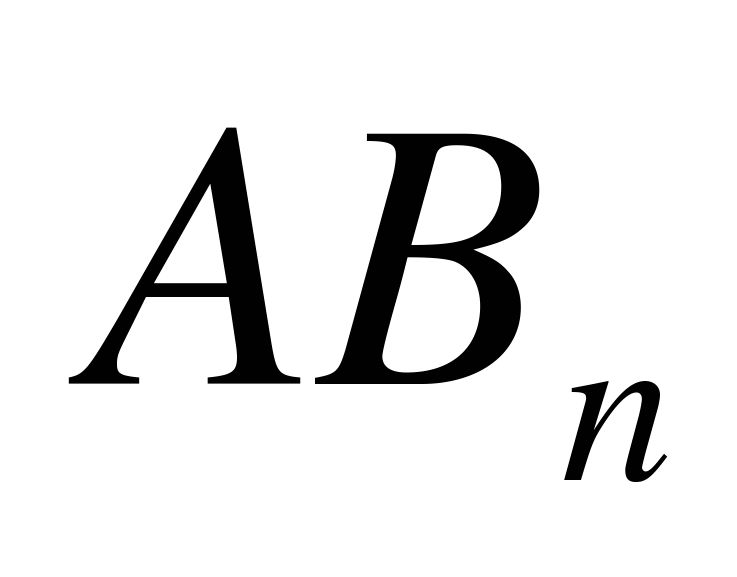. Это означает, что 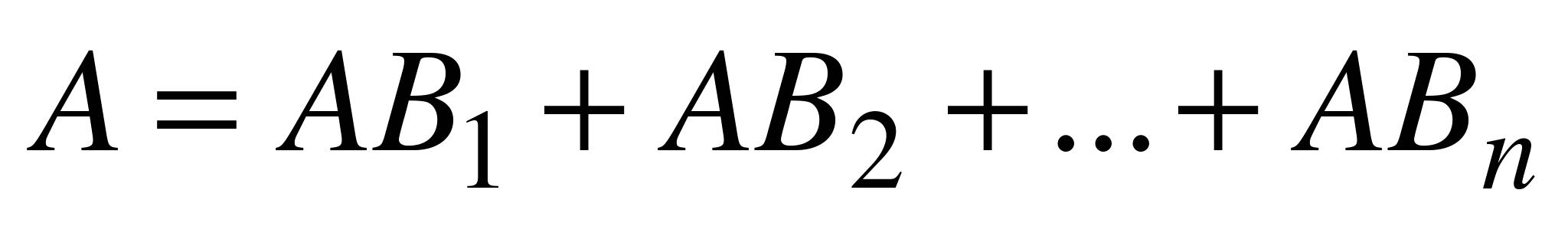. Поскольку события 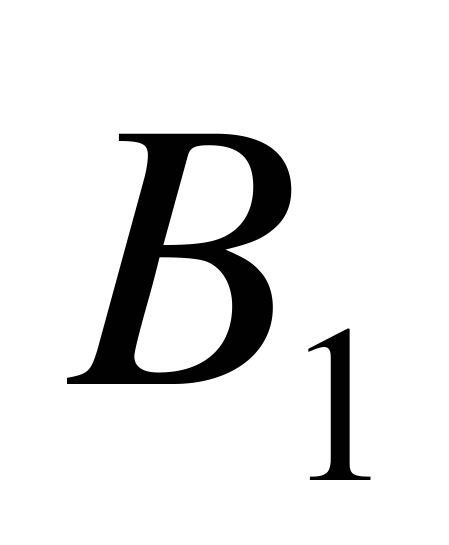, , 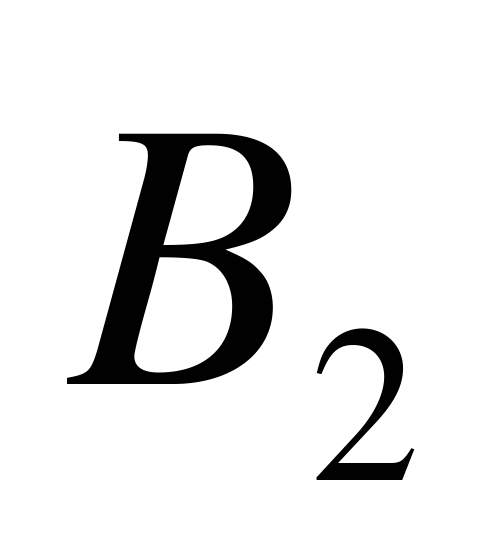… 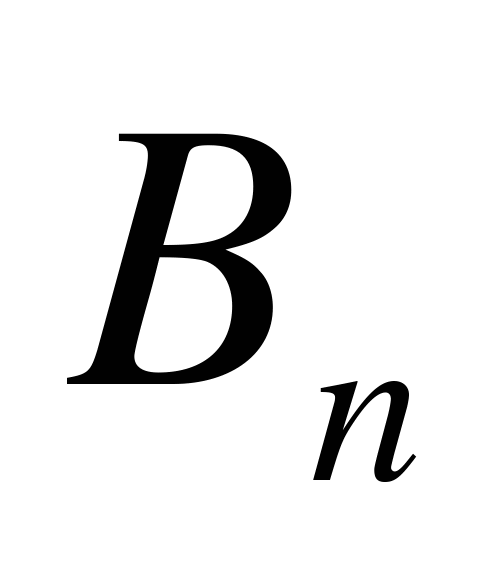попарно несовместны, то и события 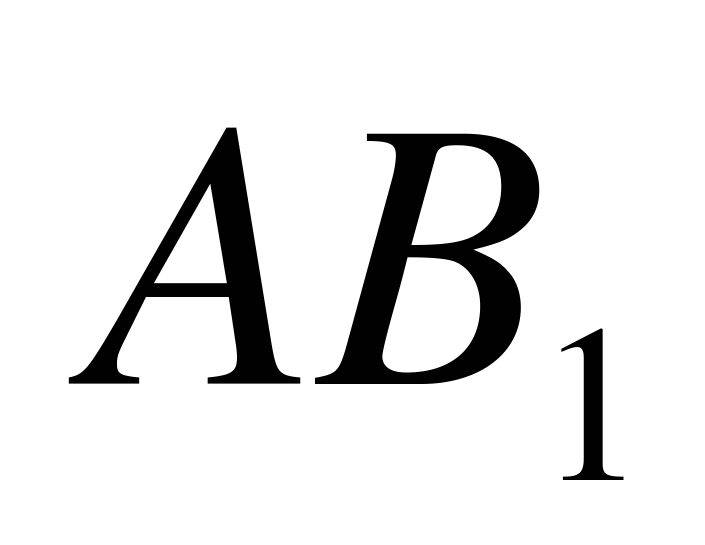, , 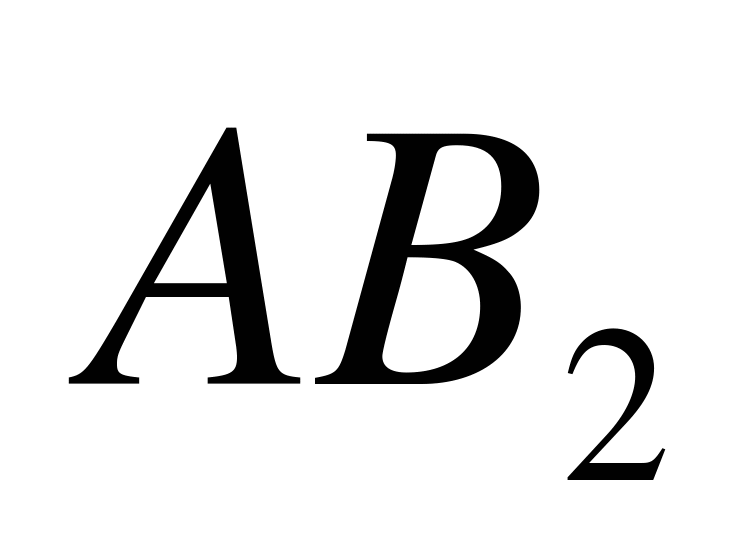… 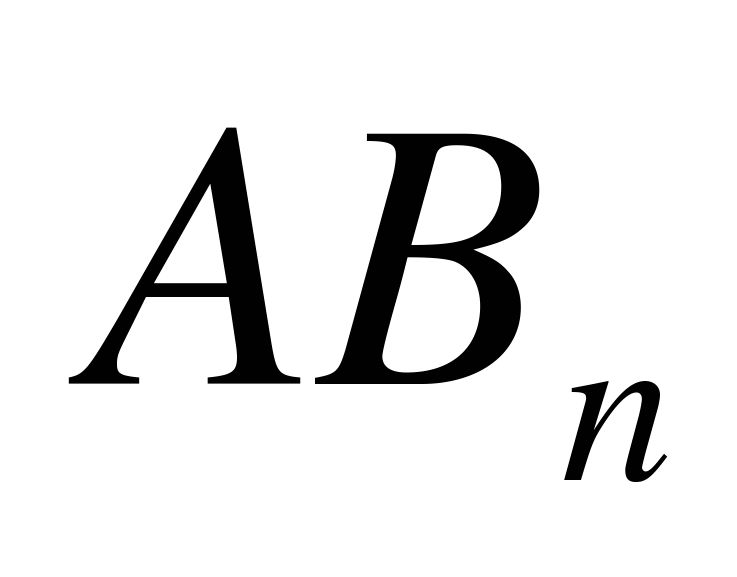обладают тем же свойством.

Согласно теореме 1, 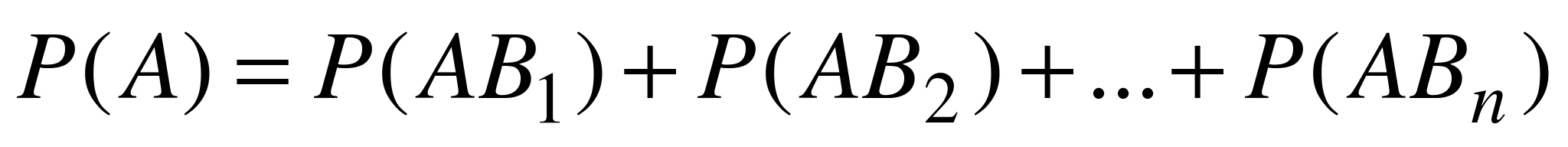. Кроме того, по формуле (4.4) имеем: 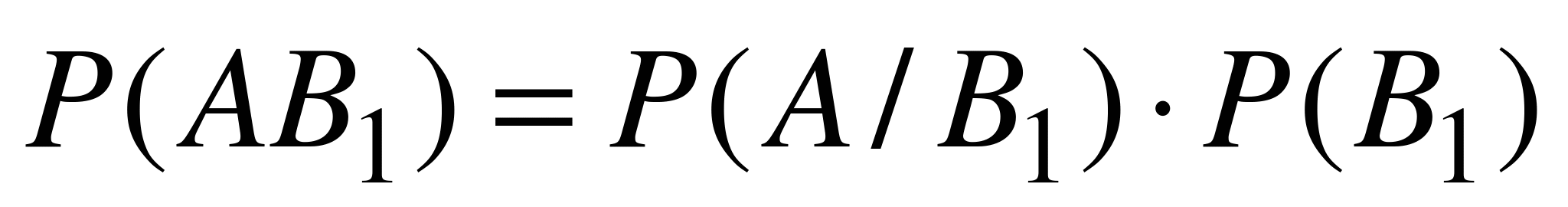, , 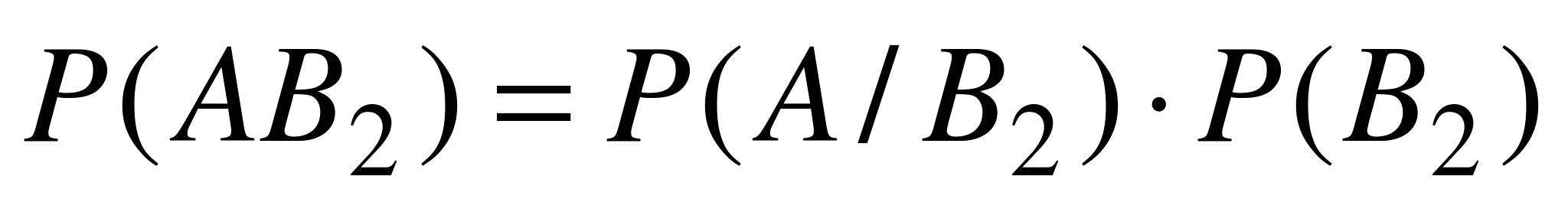…, 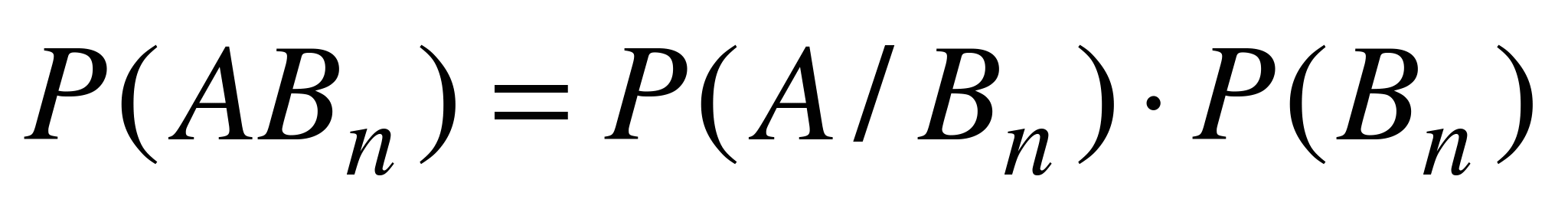. Следовательно,

 

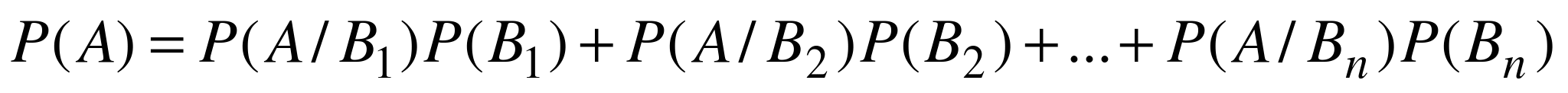. (5.1)

 

Равенство (5.1) носит название формулы полной вероятности. События 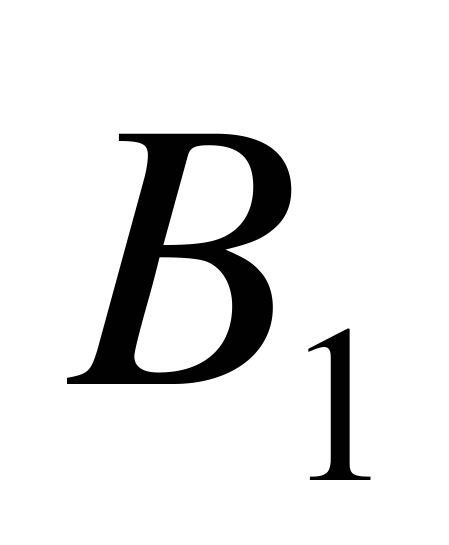, , 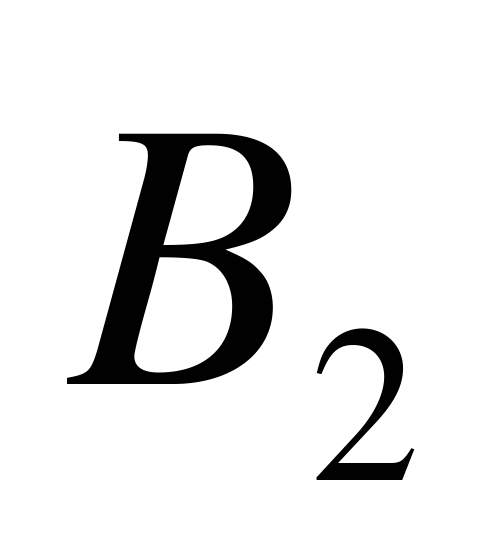… 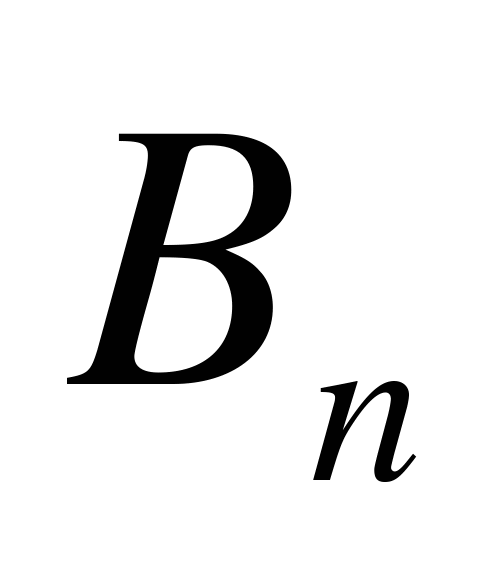в этой формуле часто называют гипотезами. Это название оправдывается тем, что мы не знаем заранее, с каким из событий 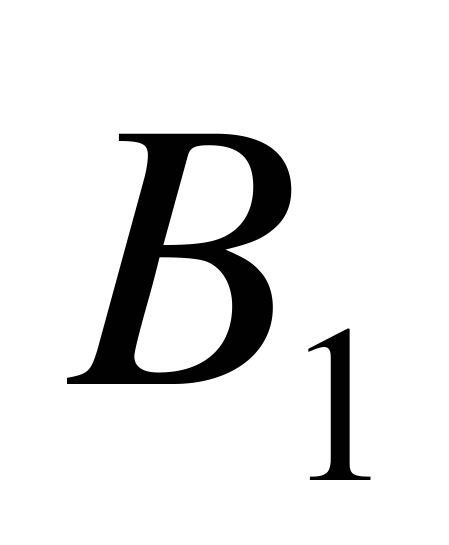, , 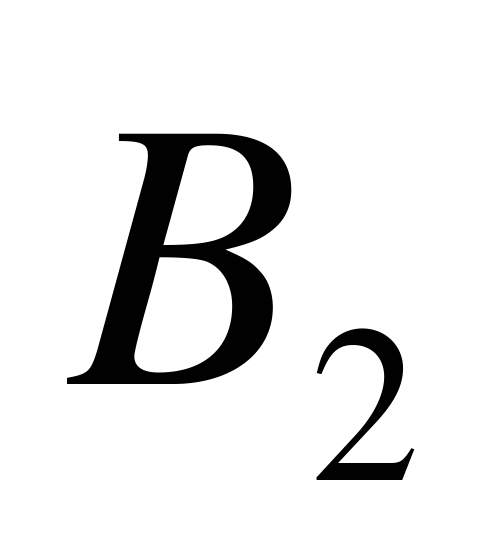… 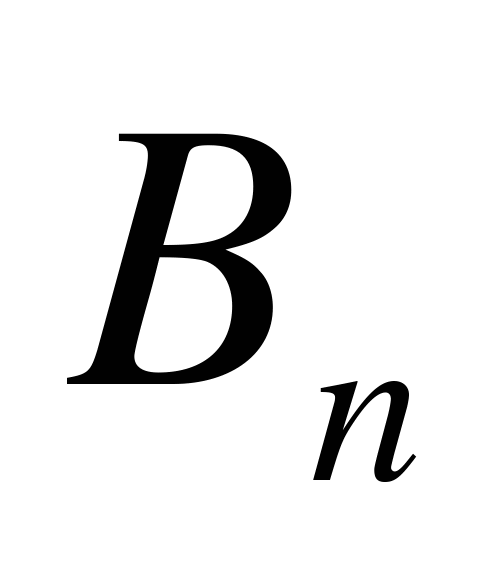вместе наступает событие А, и говорим, что А наступило в условиях той или иной гипотезы.

 

Пример 5.1. Два станка производят детали, поступающие на общий конвейер. Вероятность получения стандартной детали на первом станке равна 0,9, на втором – 0,85. Производительность второго станка вдвое больше производительности первого. Вычислим вероятность того, что наудачу взятая с конвейера деталь стандартна.

Обозначим события: А - «наудачу взятая с конвейера деталь стандартна», В₁ - «взятая деталь изготовлена на первом станке», В₂ - «деталь изготовлена на втором станке». Очевидно, что 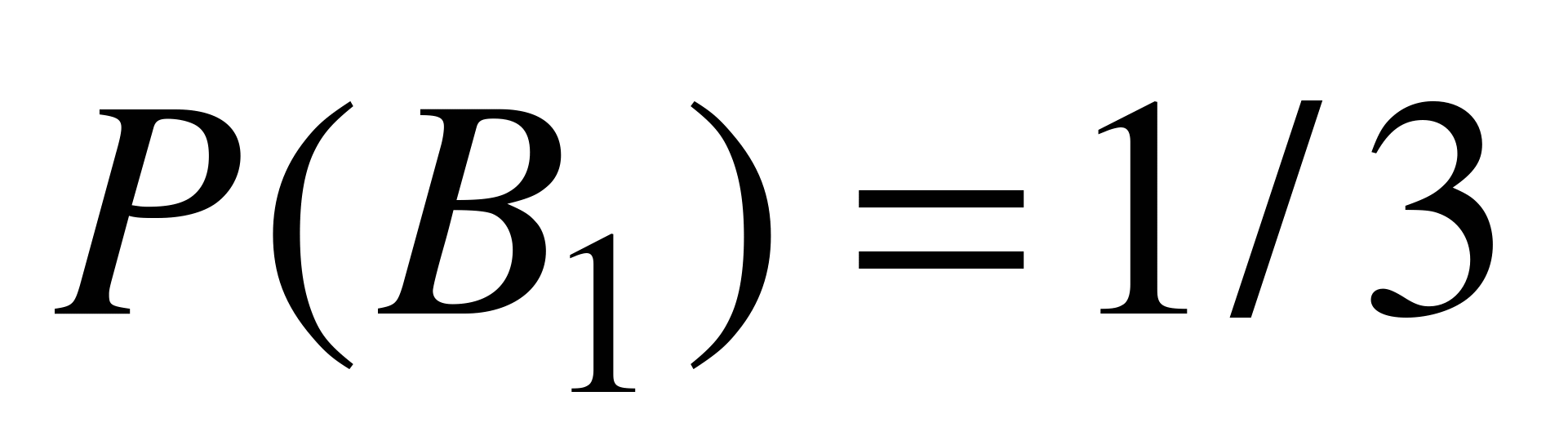, , 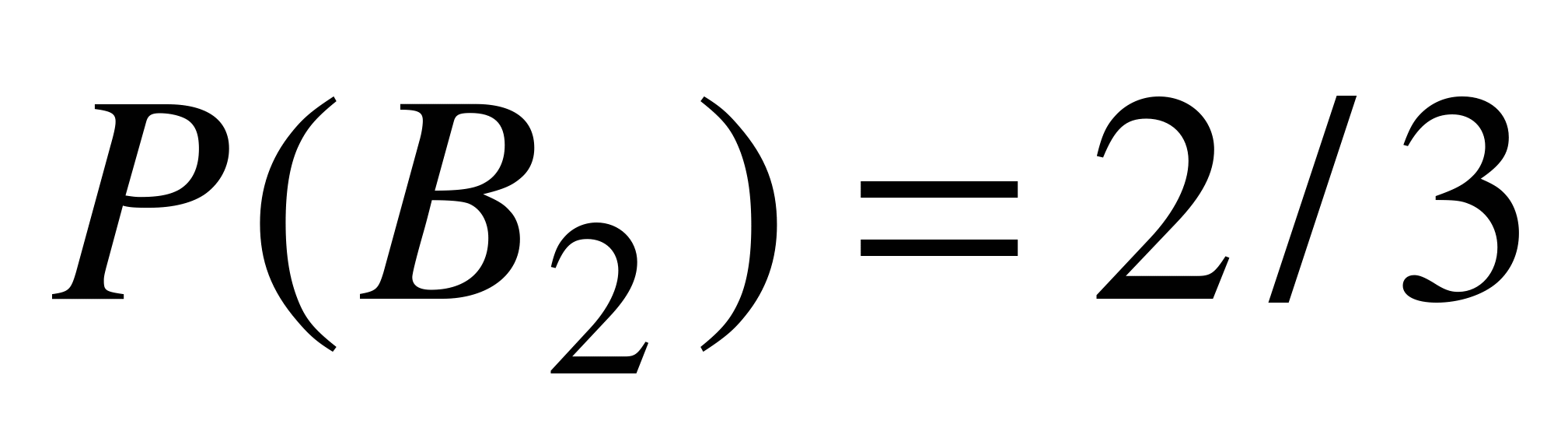, 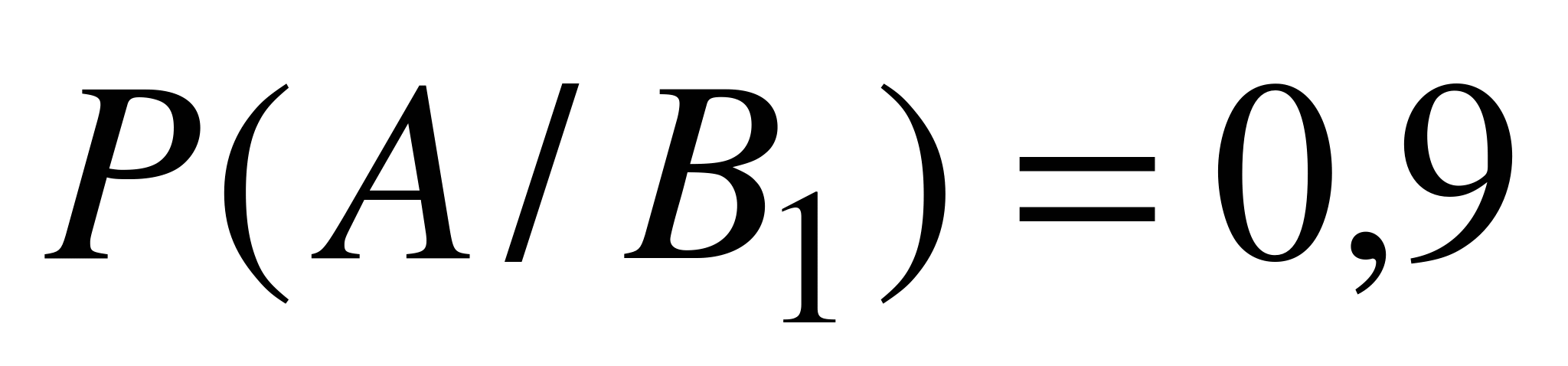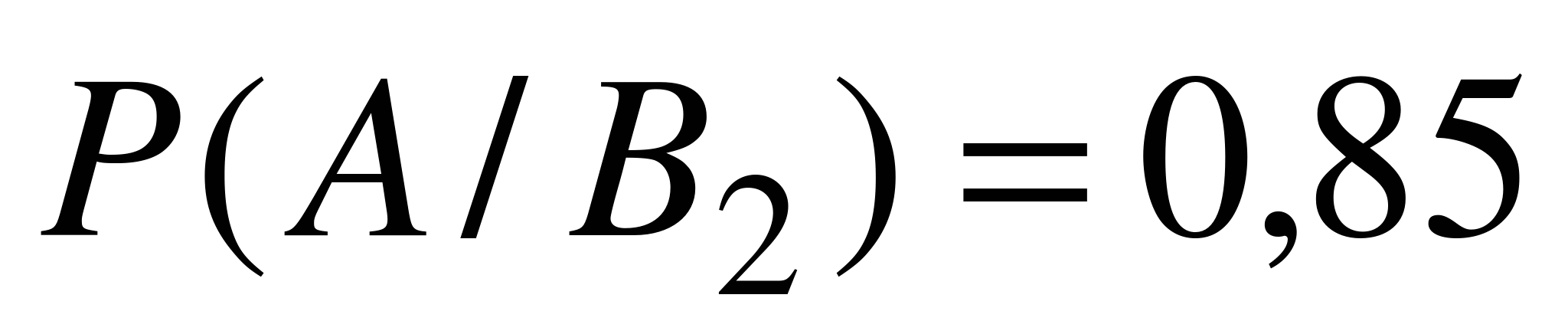. Согласно формуле полной вероятности, .

 

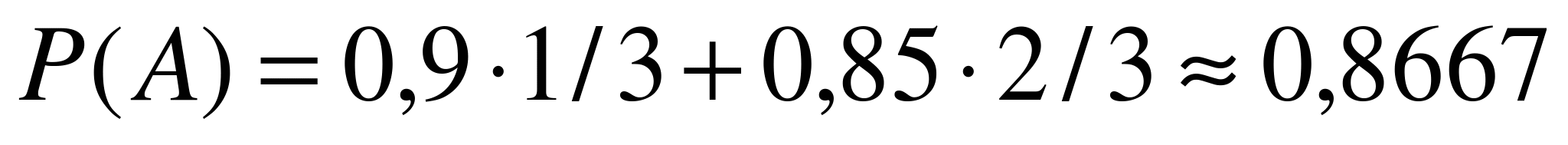Пример 5.2. Предположим, что в первой из трех урн 6 белых и 4 черных шарика, во второй – 7 белых и 3 черных, в третьей – только 8 белых. Наугад выбираем одну из трех урн, из нее наугад вынимаем шарик. Какова вероятность того, что шар белый?

Обозначим события: А – «вынут белый шарик», В₁ – «наугад выбрана первая урна», В₂ – «наугад выбрана вторая урна», В₃ – «наугад выбрана третья урна». Ясно, что 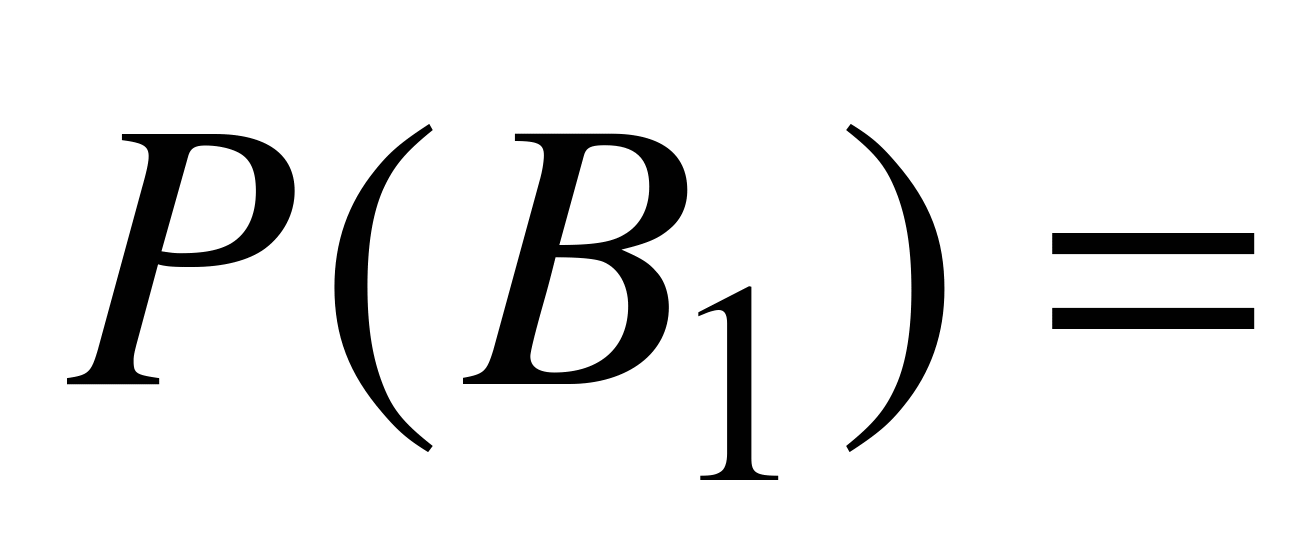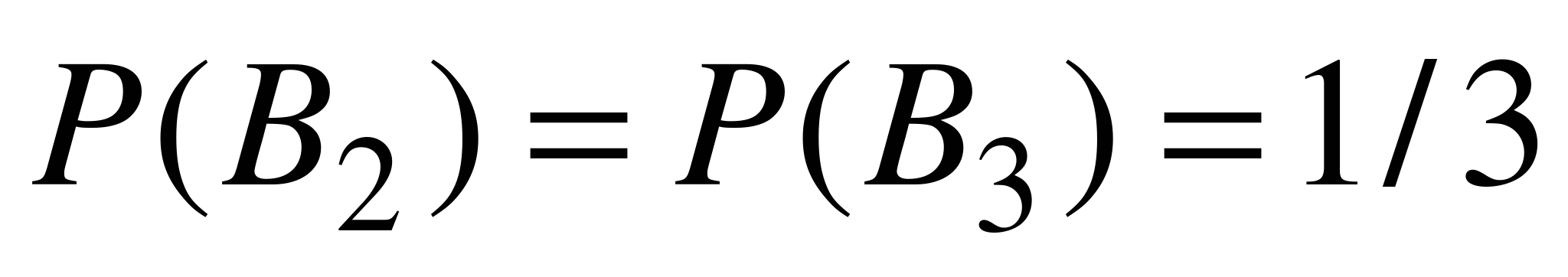, , 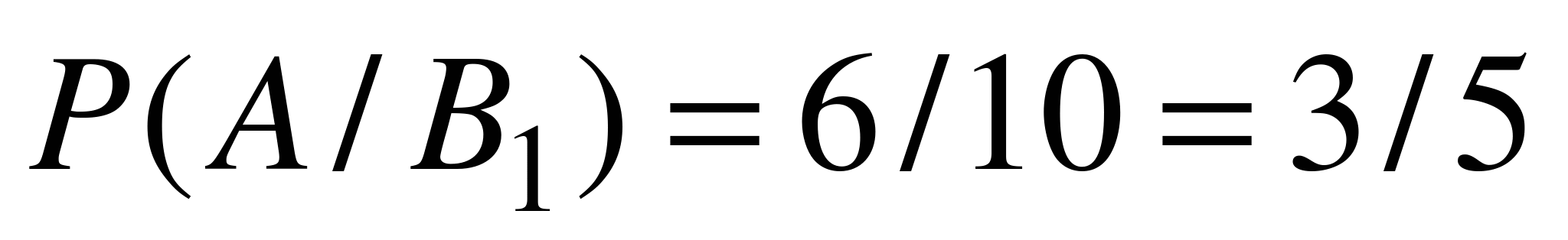, 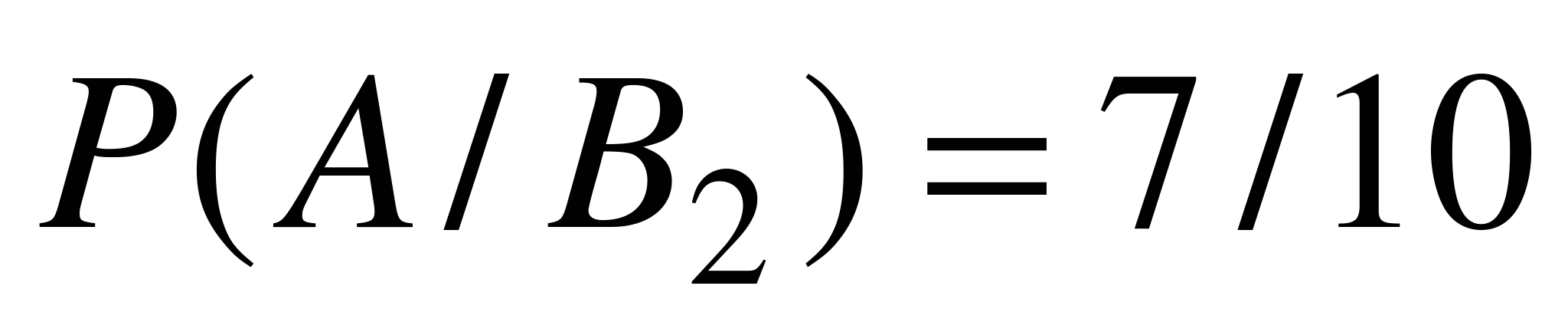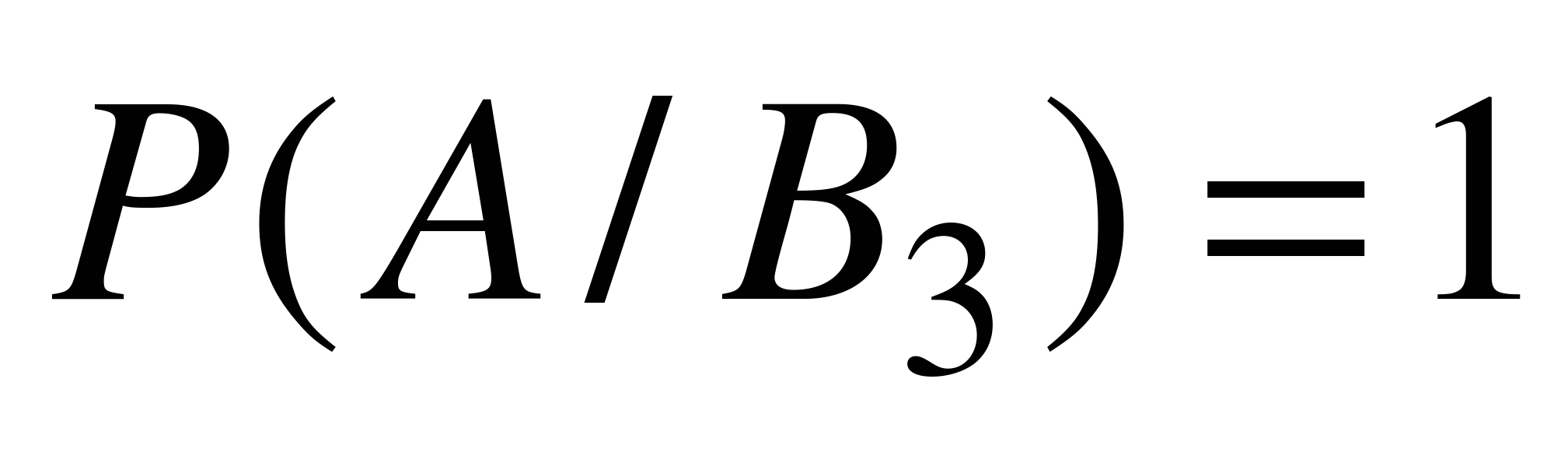. Согласно формуле полной вероятности .

 

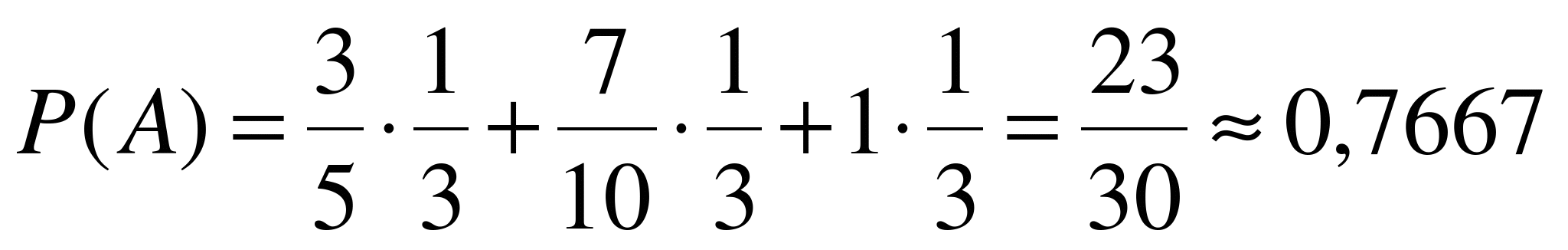Применяя формулу (5.1) легко найти вероятность 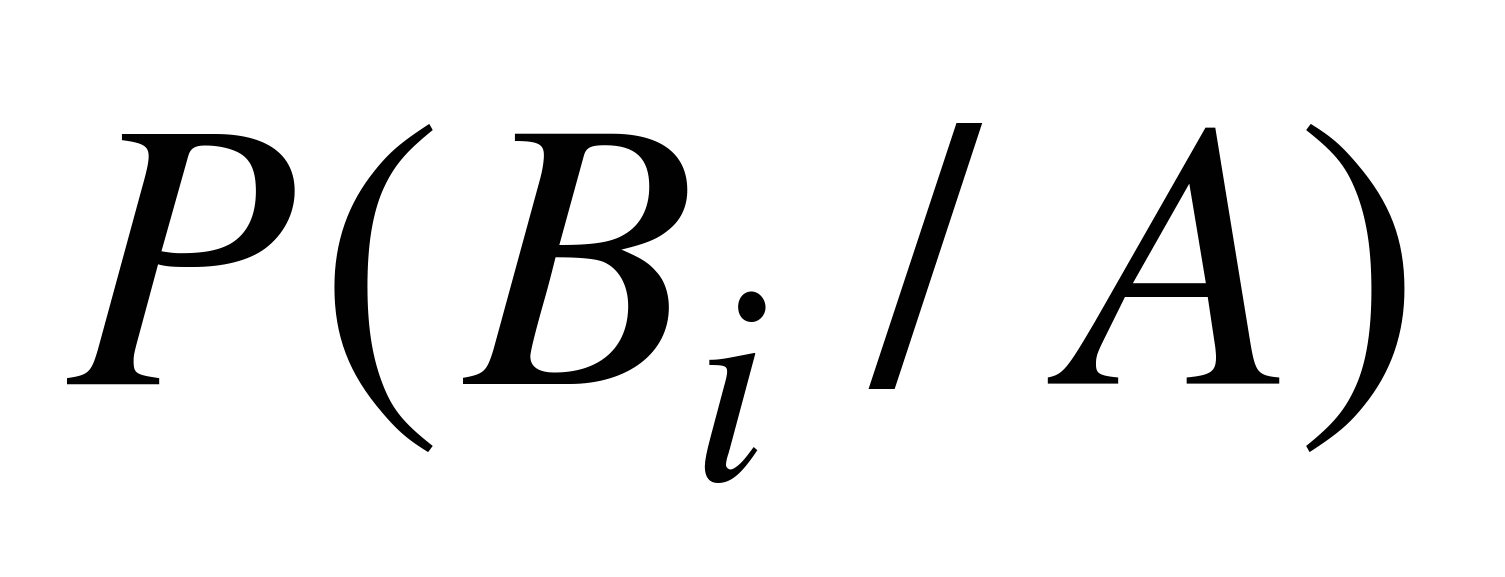для любого i от 1 до n. Действительно, 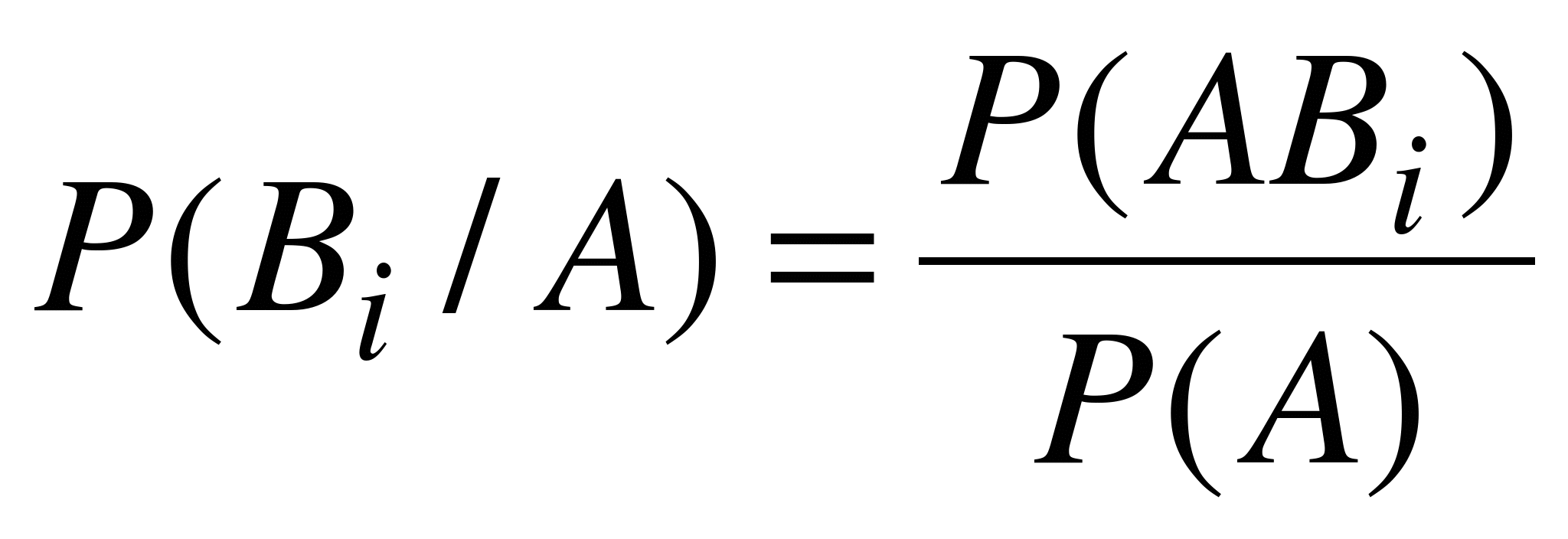. Подставляя в эту формулу значение 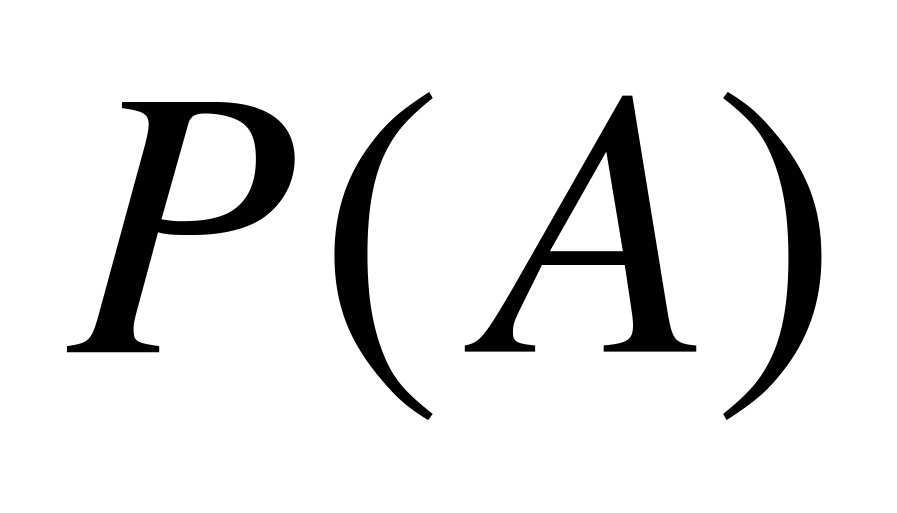из (5.1) и учитывая, что , получаем

 

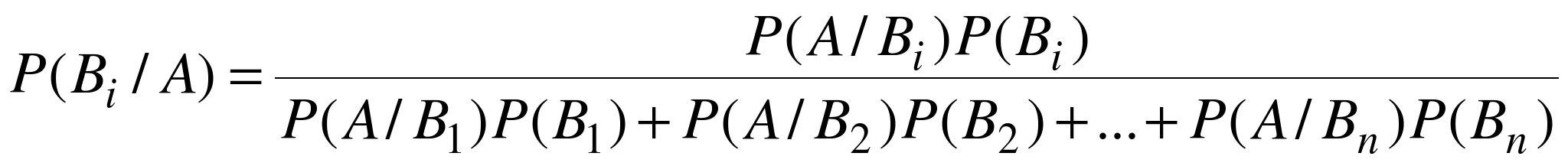. (5.2)

 

Формула (5.2) называется формулой Байеса. Она широко применяется при решении задач, связанных с вероятностной оценкой гипотез после проведения эксперимента, поскольку позволяет найти вероятность каждой гипотезы при условии, что событие А произошло.

Опишем общую схему применения формулы Байеса.

Пусть событие А происходит в различных условиях, относительно которых может быть сделано n гипотез: 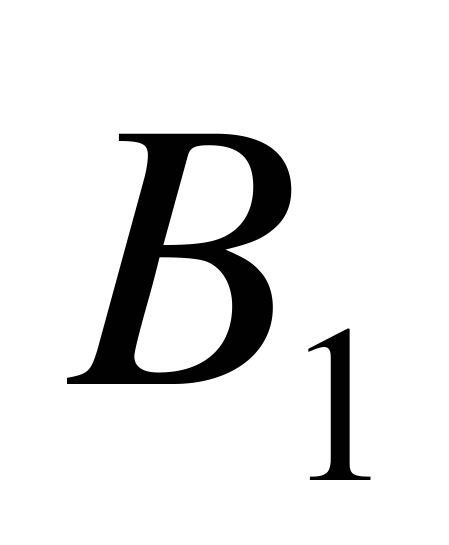, , 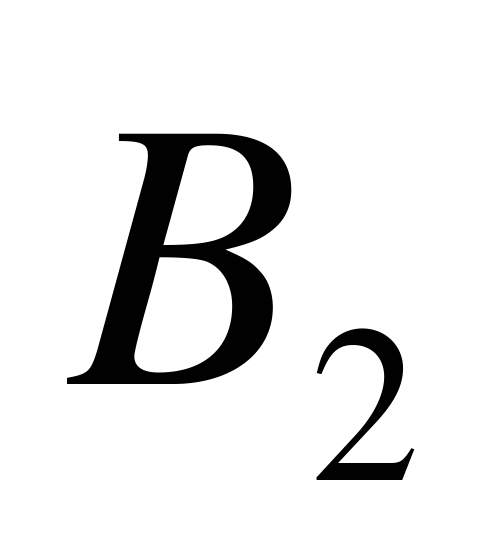… 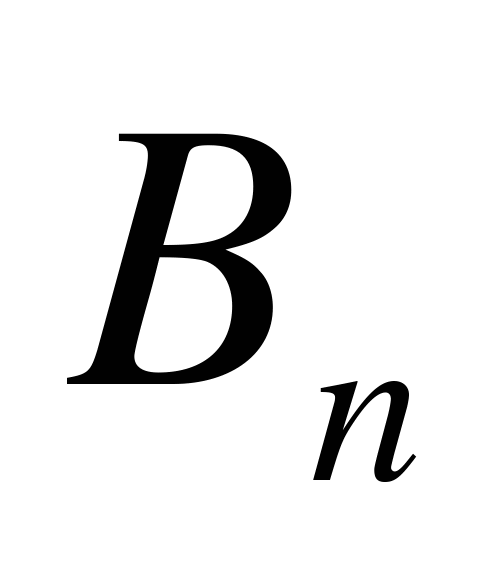. Пусть нам известны вероятности 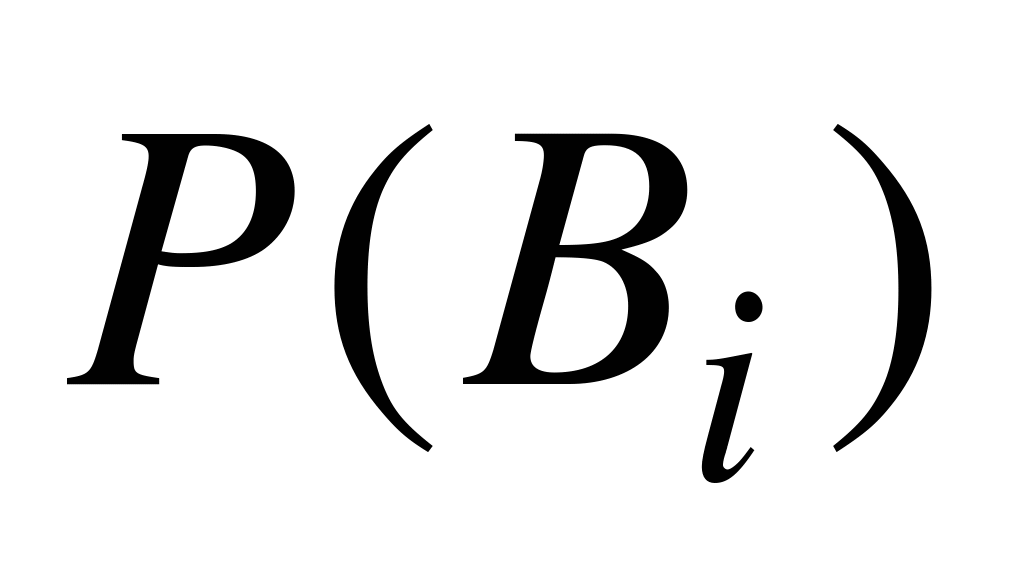этих гипотез до испытания. Известно также, что в условиях гипотезы 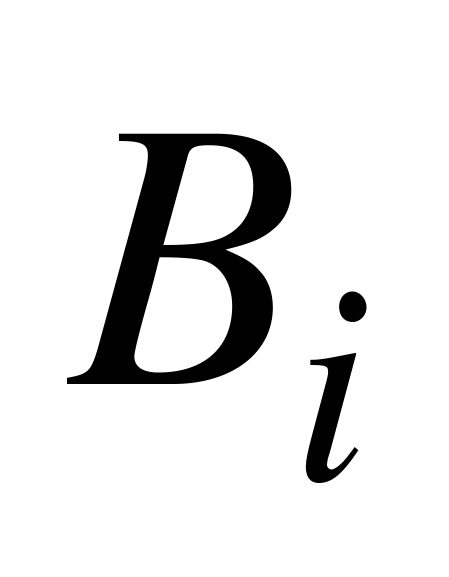событие А имеет вероятность 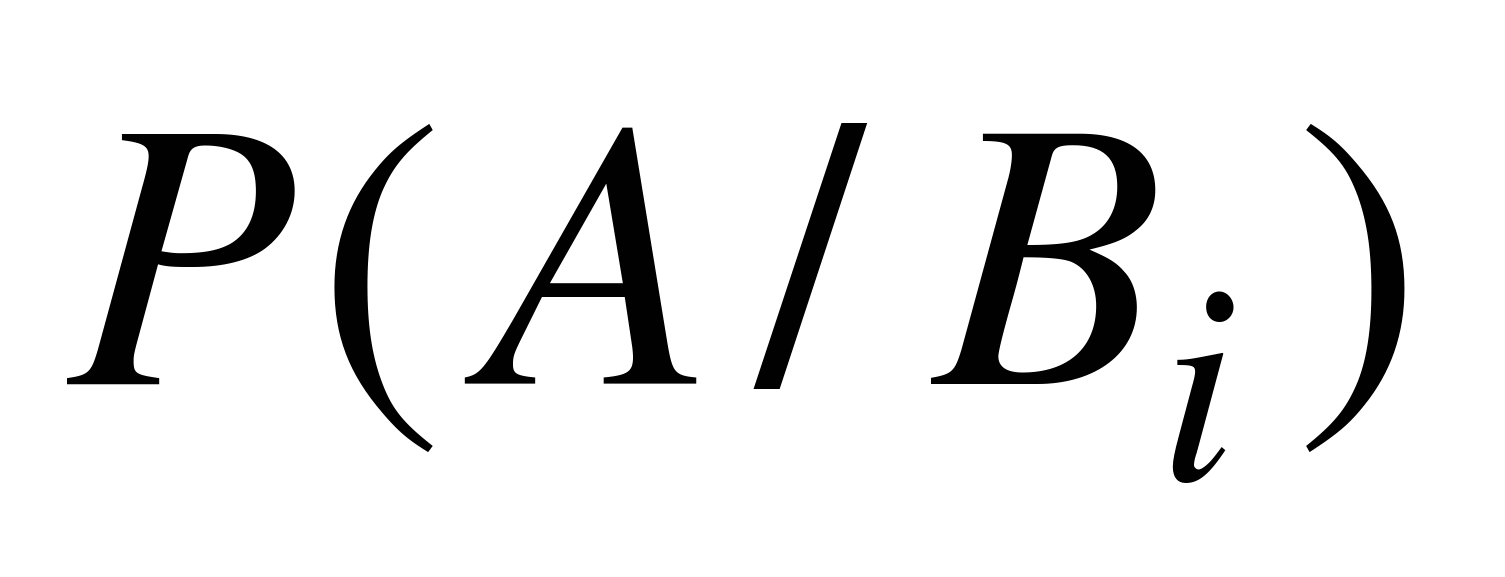. Произведен опыт, в котором событие А наступило. Как оценить вероятность того, что оно произошло в условиях определенной гипотезы? Ответ на этот вопрос и дает формула (5.2).

 

Пример 5.3. В первой из трех урн 6 белых и 4 черных шарика, во второй – 7 белых и 3 черных, в третьей – только 8 белых. Наугад выбираем одну из трех урн, из нее наугад вынимаем шарик. Он оказался белым. Какова вероятность того, что шар вынут из второй урны?

Обратите внимание на то, что формулировки задач 5.2 и 5.3 очень похожи. Они отличаются лишь поставленными вопросами. В первой из этих задач надо вычислить вероятность события А, которое происходит в условиях гипотез 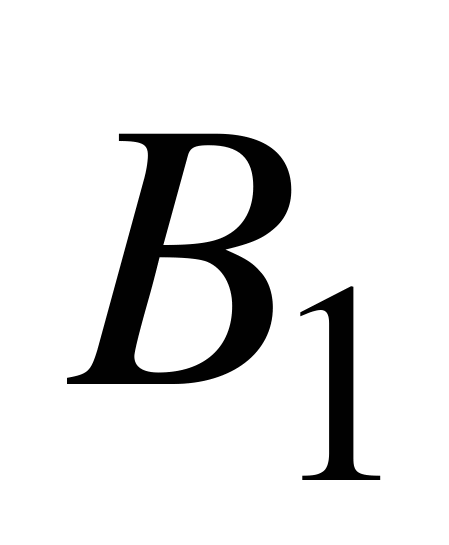, 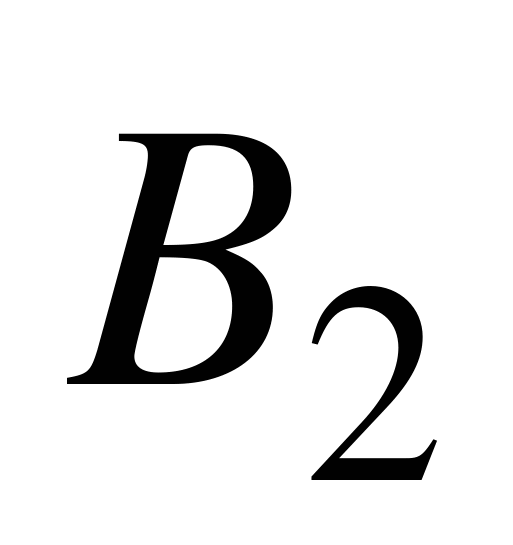и 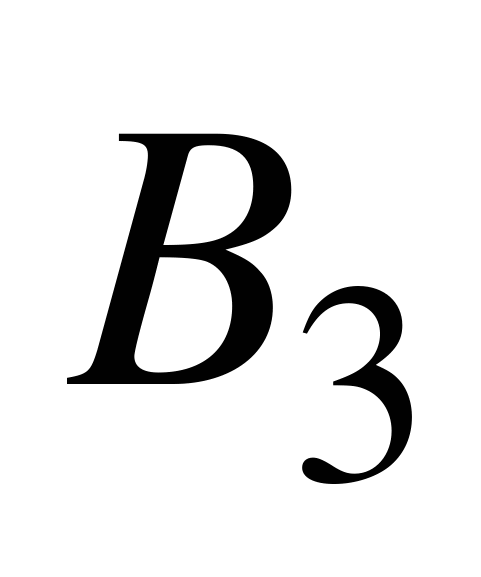, и поэтому мы применяем формулу полной вероятности. Во второй задаче событие А уже произошло, требуется переоценить вероятность второй гипотезы, т.е. вычислить 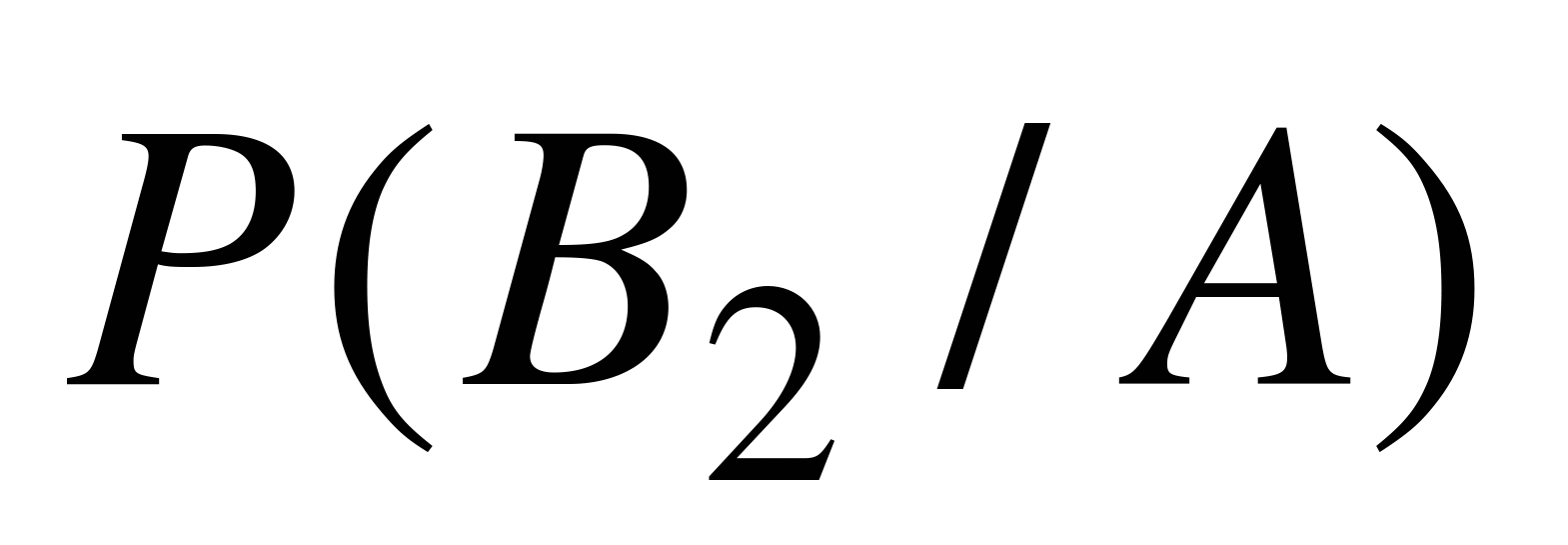, значит, здесь нужно применить формулу Байеса.

События обозначаем так же, как и в задаче 5.2: А – «вынут белый шарик», В₁ – «наугад выбрана первая урна», В₂ – «наугад выбрана вторая урна», В₃ – «выбрана третья урна». Тогда 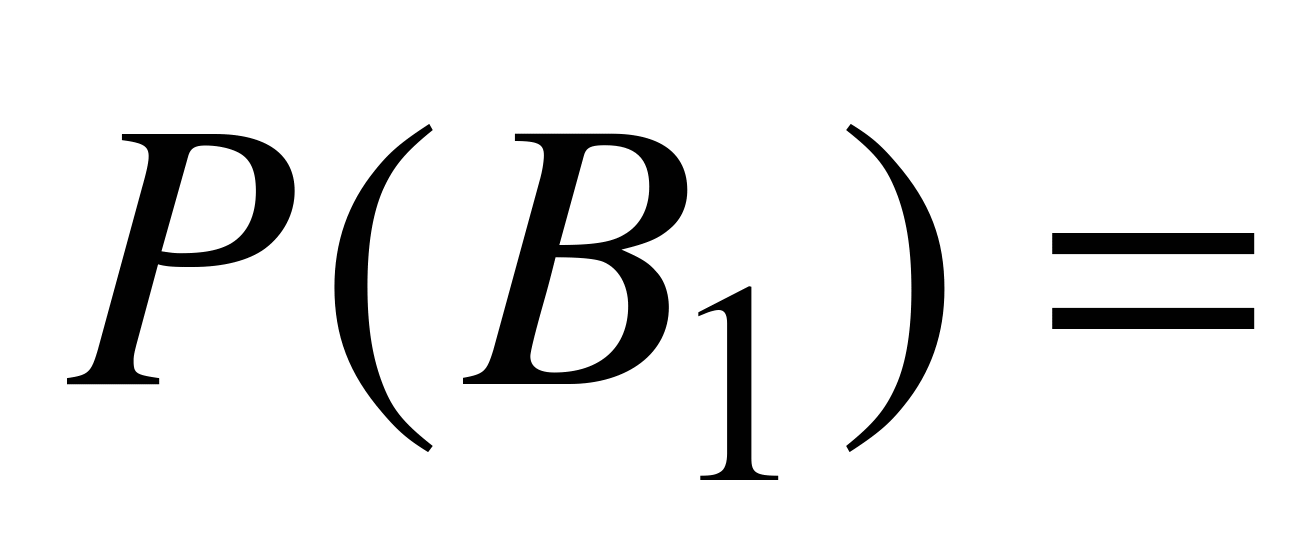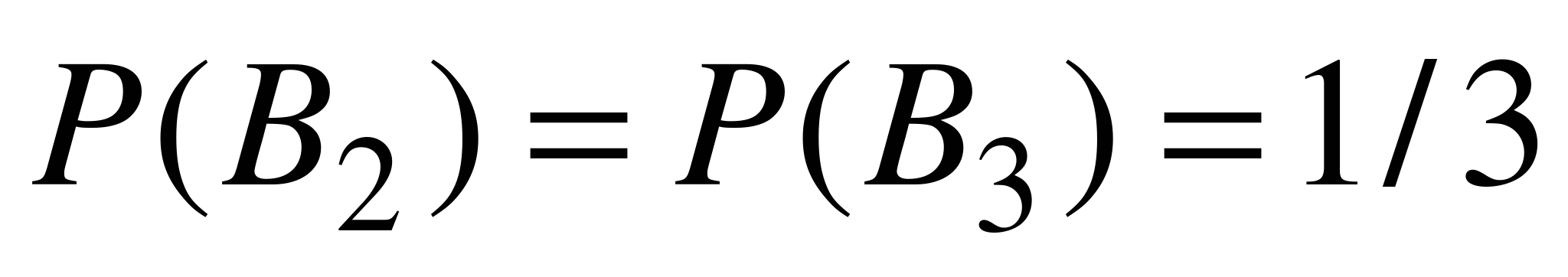, , 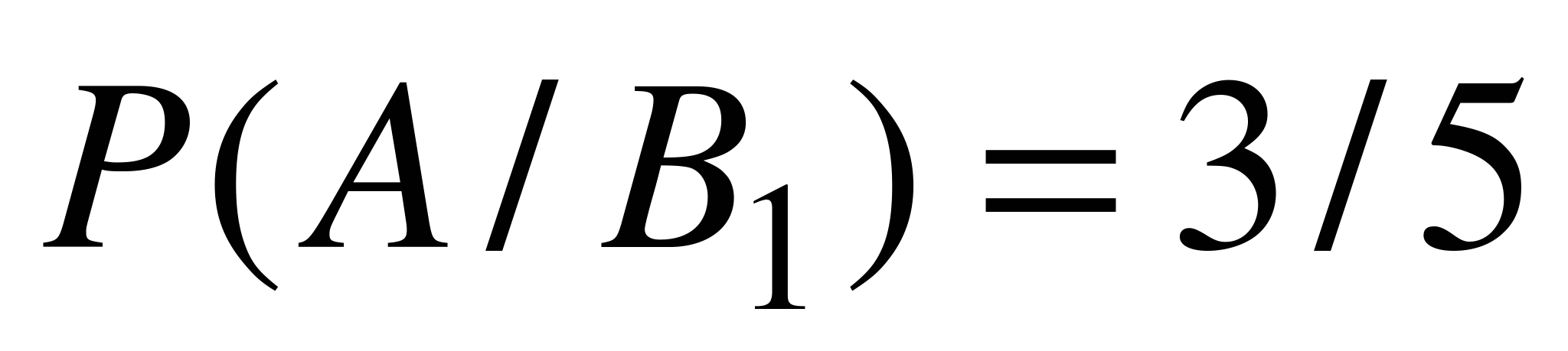, 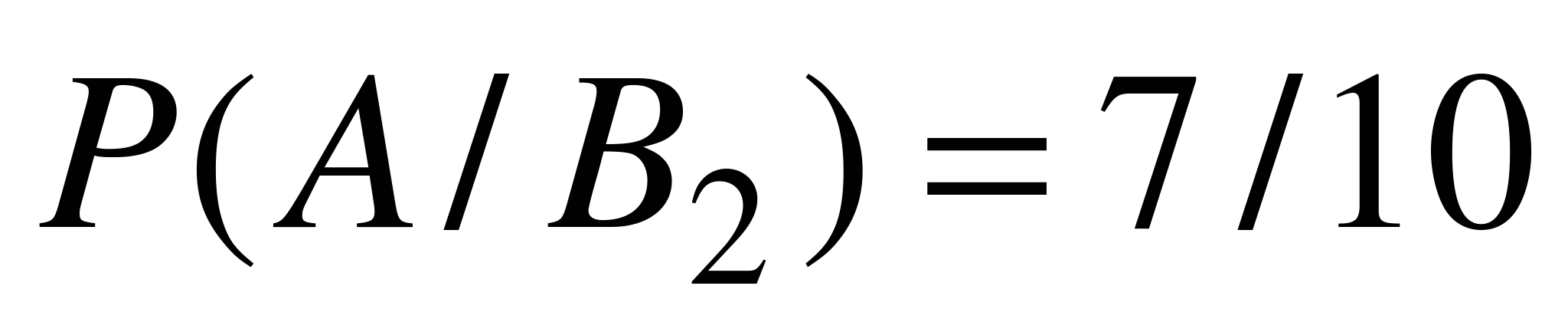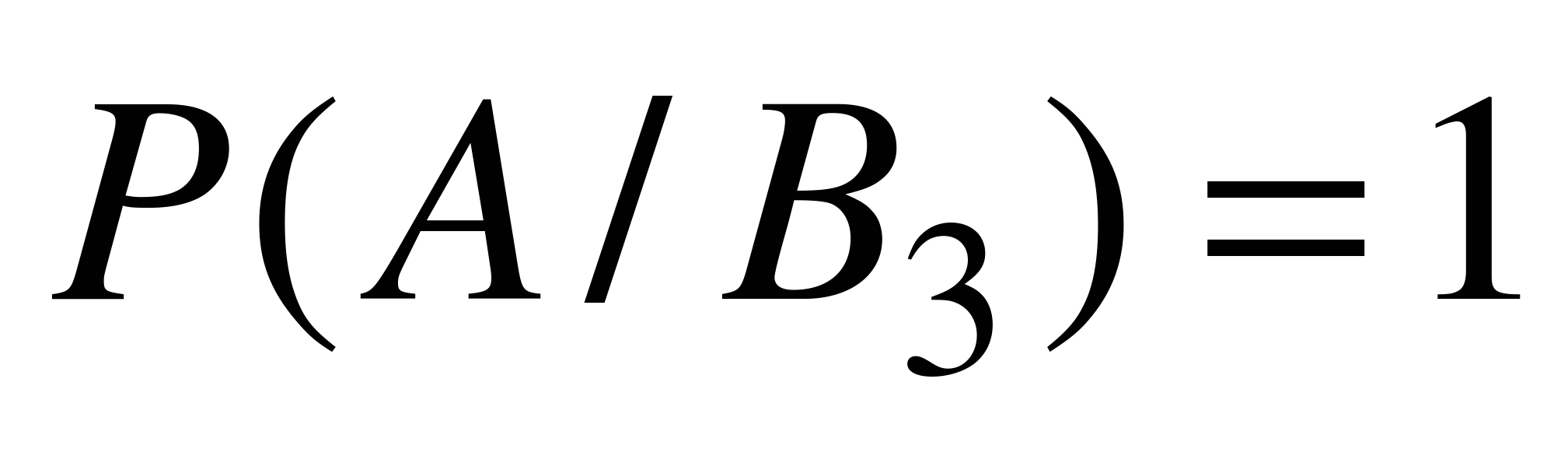. Согласно формуле Байеса .

 

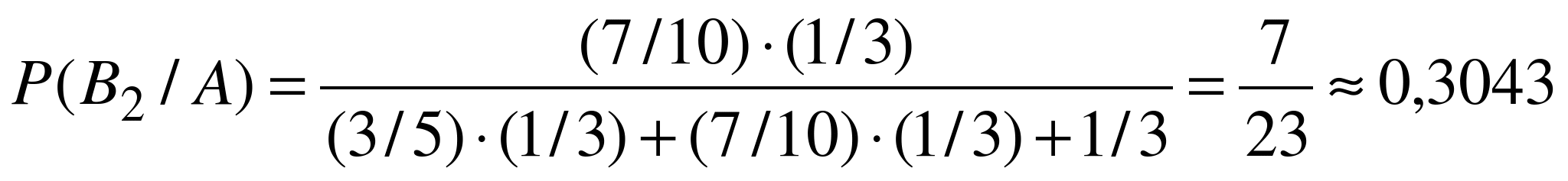Проиллюстрируем применение формулы (5.2) еще на одном примере.

 

Пример 5.4. Из 10 студентов, которые пришли на экзамен по математике, трое подготовились отлично, четверо – хорошо, двое – удовлетворительно, а один совсем не подготовился – понадеялся на то, что все спишет. В билетах 20 вопросов. Отлично подготовившиеся студенты могут ответить на все 20 вопросов; те, кто подготовился хорошо, могут ответить на 16 вопросов; удовлетворительно – на 10; а тот, кто не подготовился, может ответить только на 5 вопросов. Каждый студент получает билет, в котором три вопроса. Приглашенный первым студент ответил на все вопросы своего билета. Какова вероятность того, что он отлично подготовился?

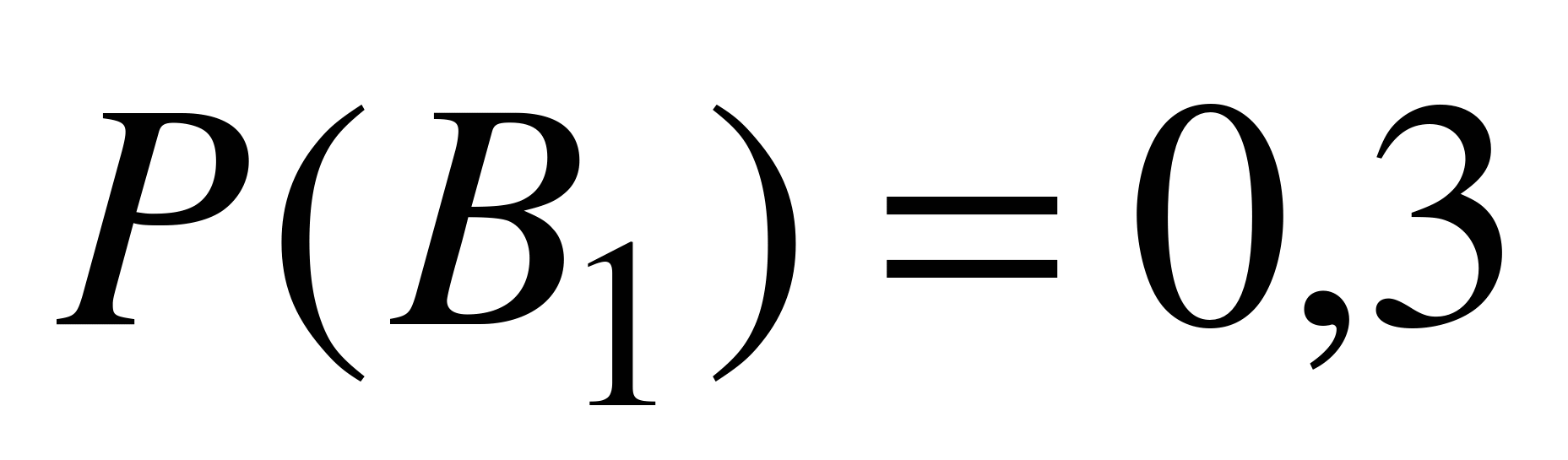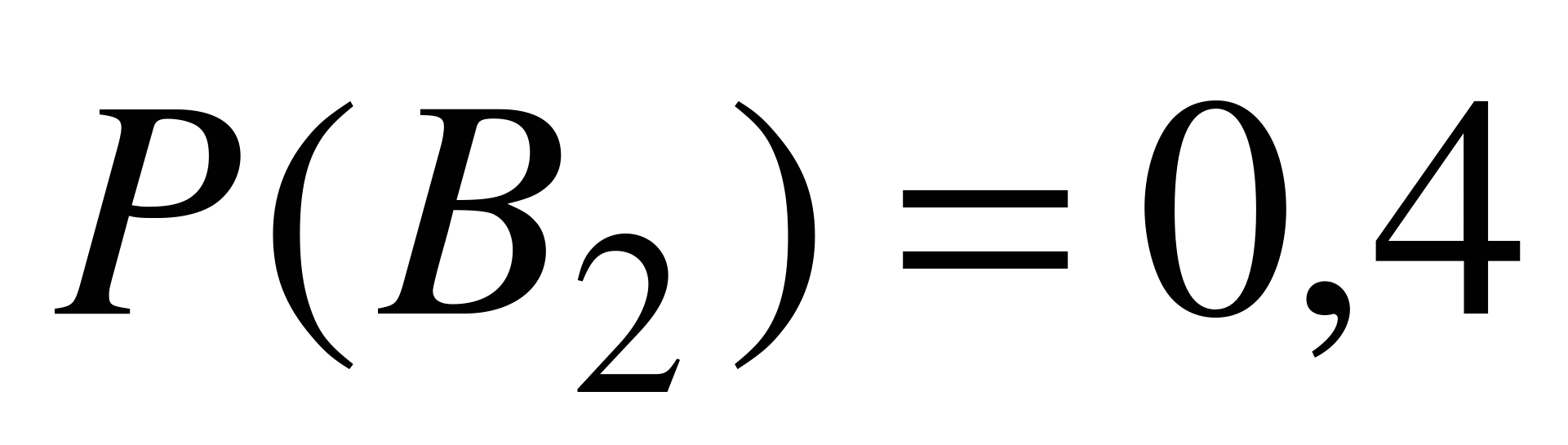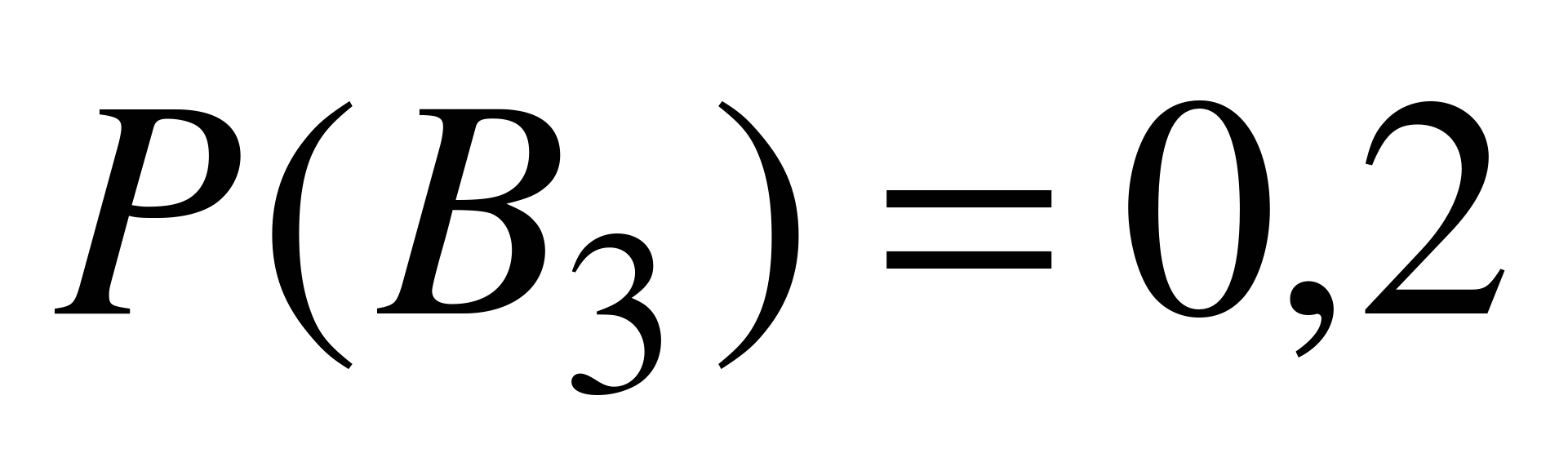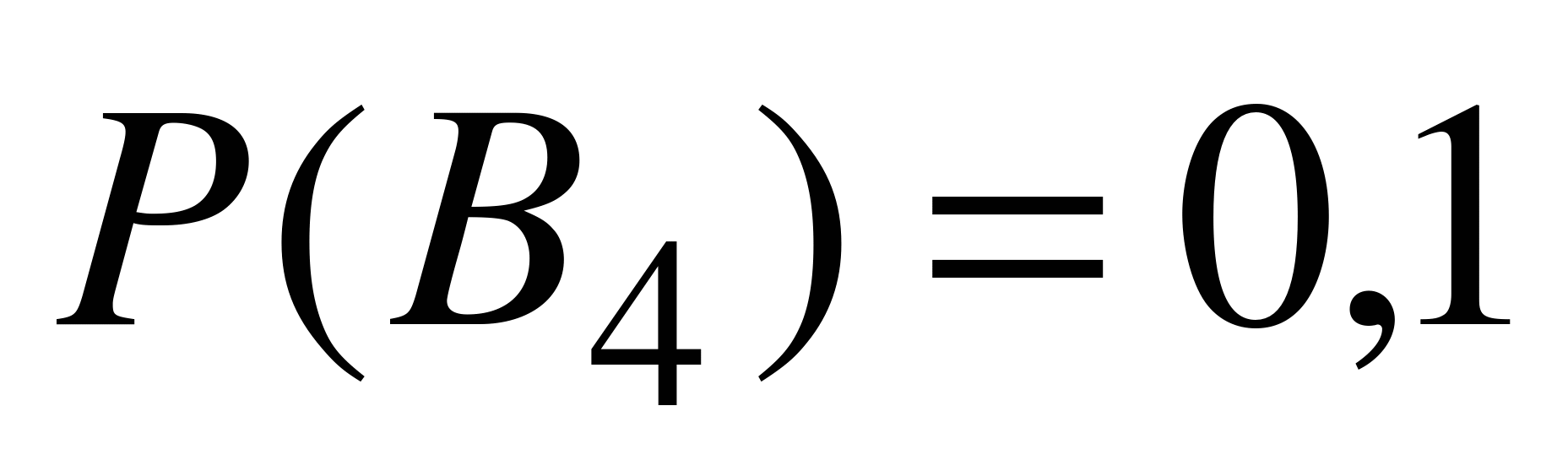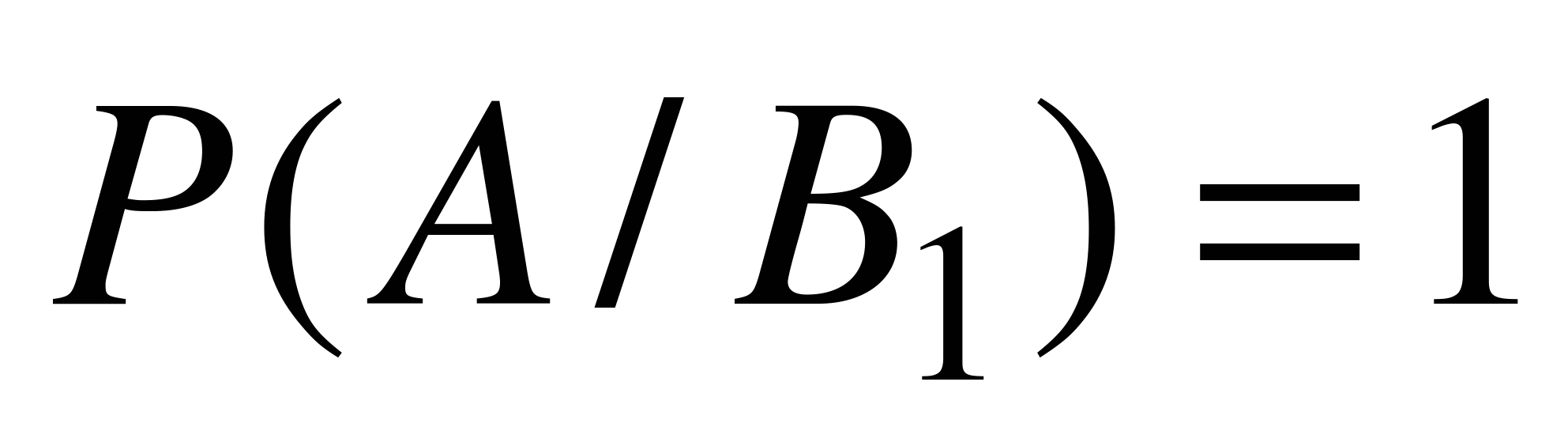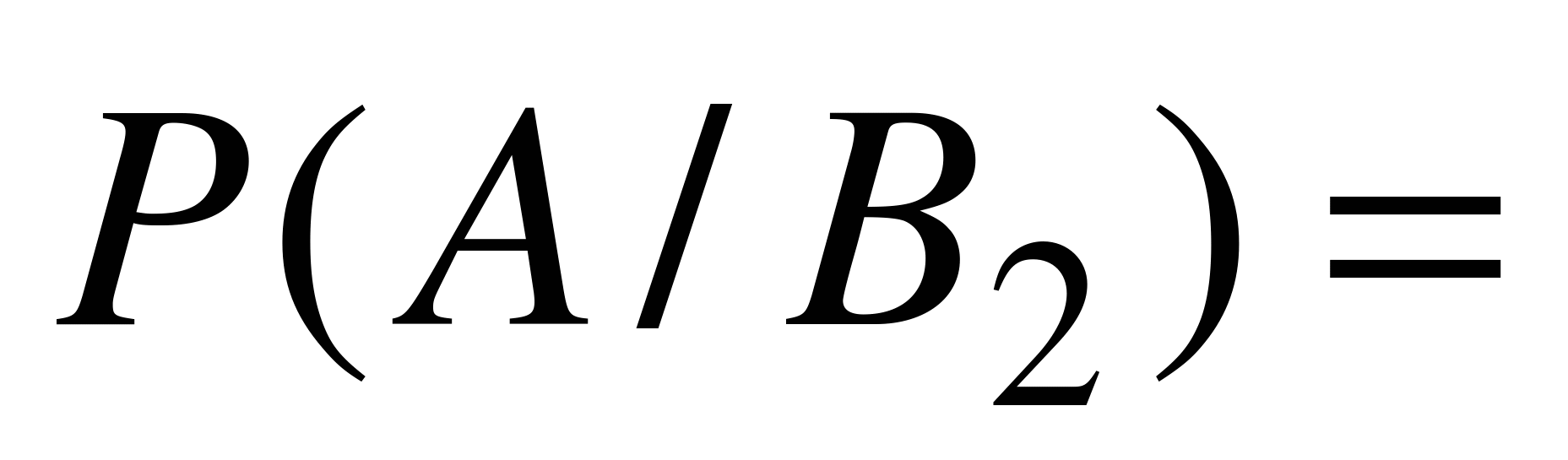
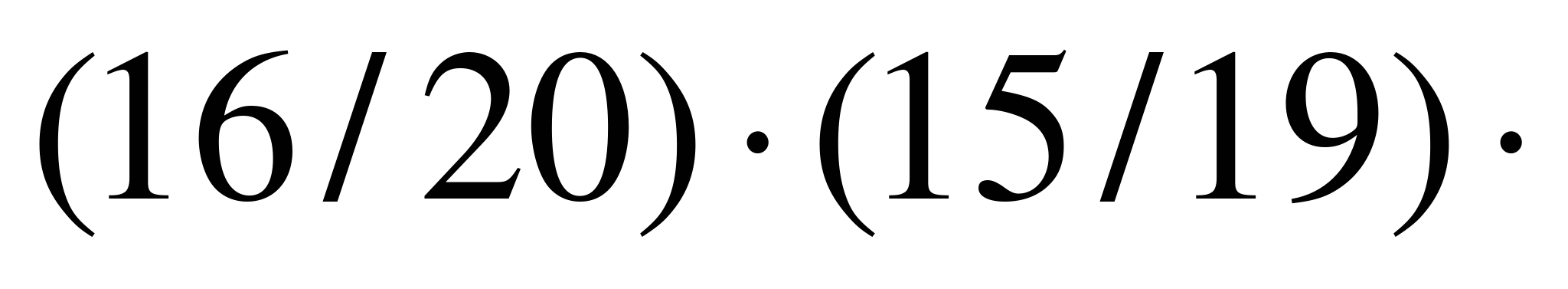
Обозначим события: А- «студент ответил на 3 вопроса», В₁ – «приглашен студент, подготовившийся отлично», В₂ – «приглашен студент, подготовившийся хорошо», В₃ – «приглашен студент, подготовившийся удовлетворительно», В₄ – «приглашен студент, который к экзамену не готов». Согласно условиям задачи, , , , . Кроме того, , , 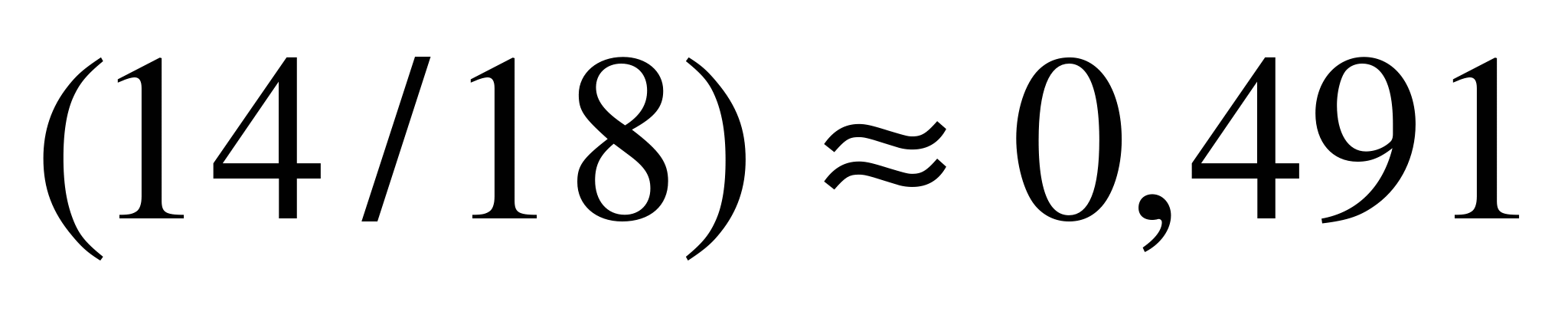, 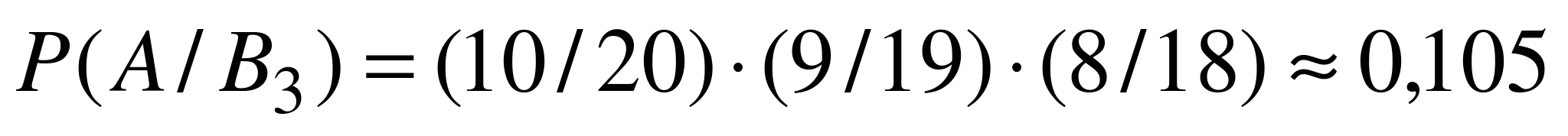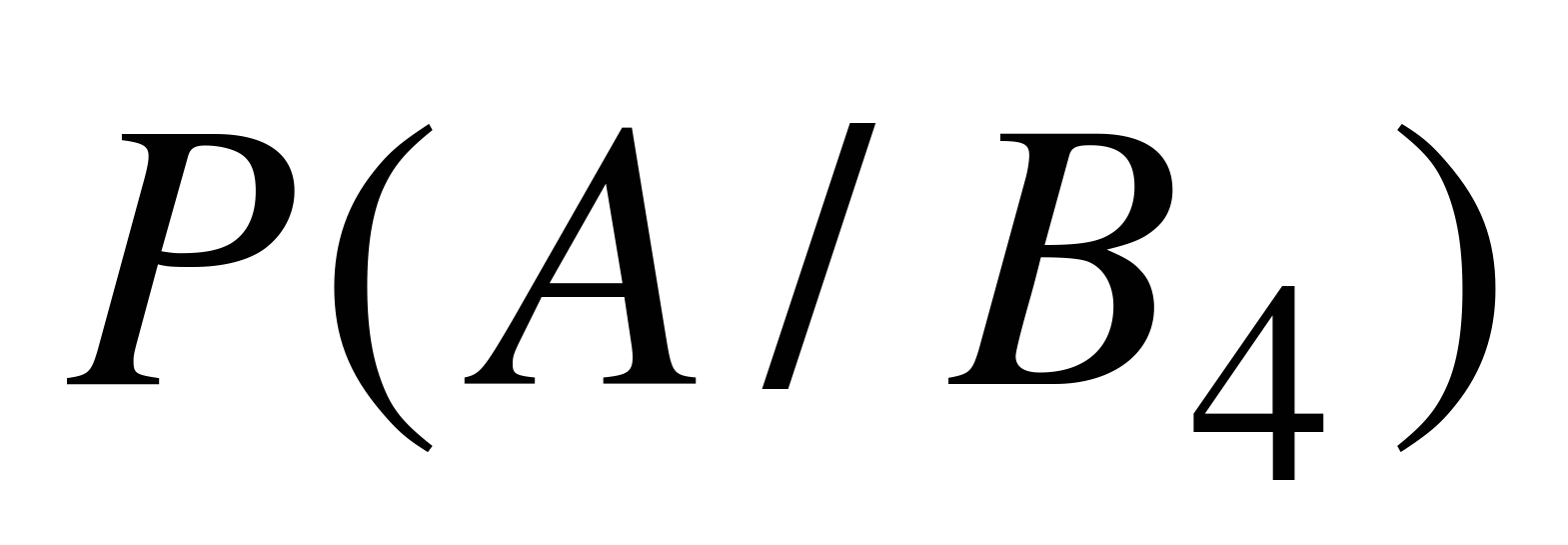= 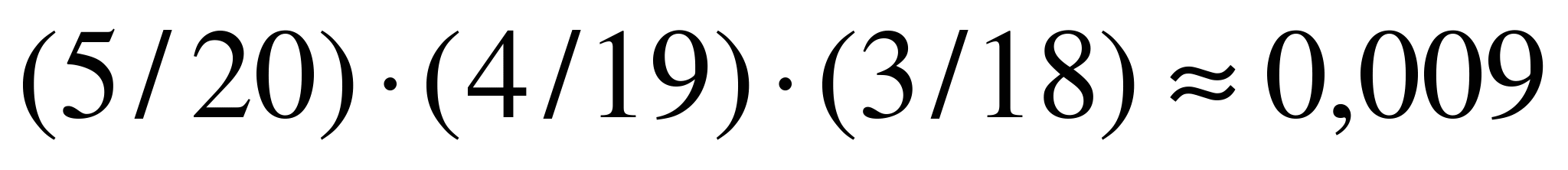. Следует найти 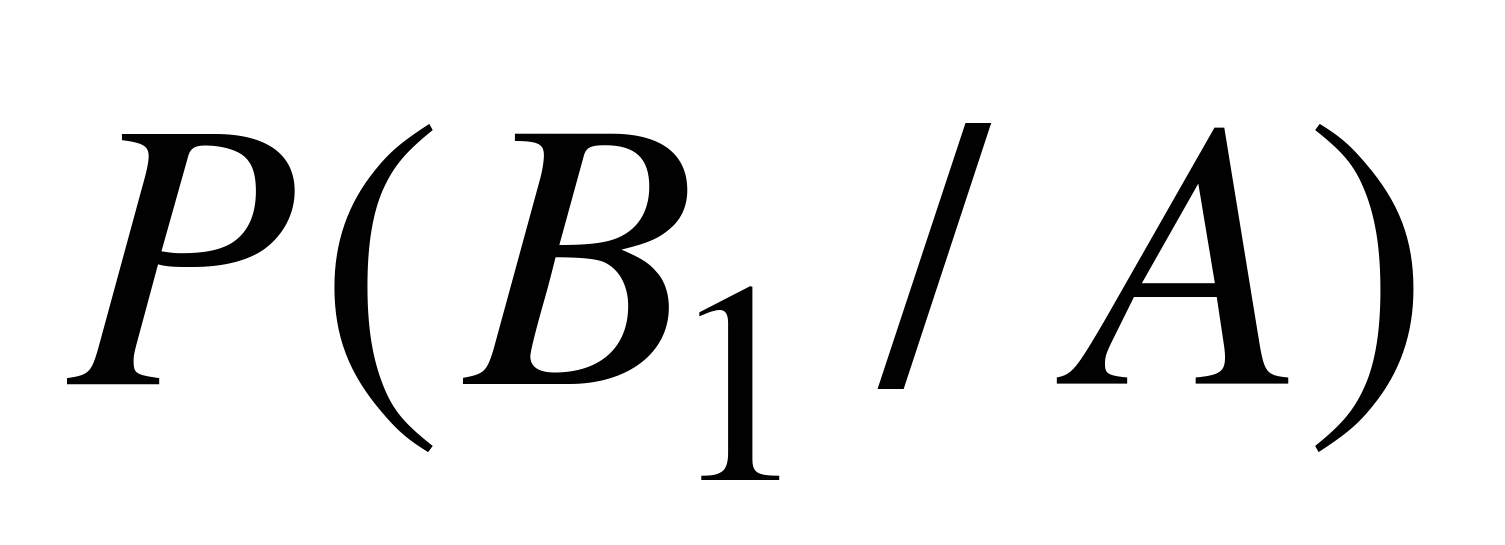. По формуле Байеса

.

 

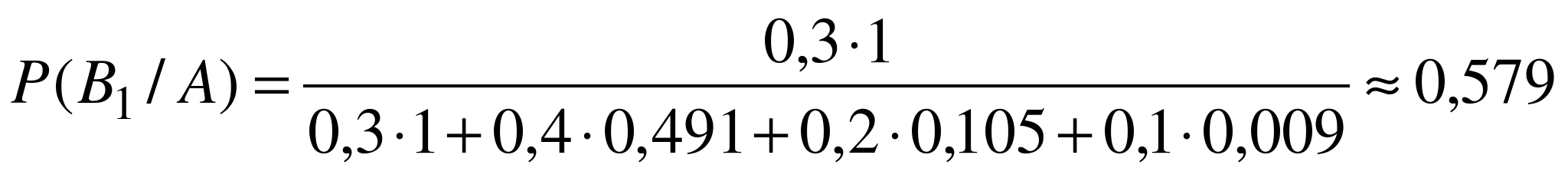Как видим, искомая вероятность сравнительно невелика, поэтому преподавателю придется предложить студенту еще несколько дополнительных вопросов.