Оценка статистической значимости регрессии

Перейдем к вопросу о том, как отличить "хорошие" оценки МНК от "плохих". Конечно, предполагается, что существуют критерии качества рассчитанной линии регрессии.

Перечислим способы, которые помогают решить вопрос о достоинствах рассчитанной линии регрессии:

§ построение доверительных интервалов и оценка статистической значимости коэффициентов регрессии по t-критерию Стьюдента;

§ дисперсионный анализ и F – критерий Фишера;

§ проверка существенности выборочного коэффициента корреляции (детерминации).

Перейдем к подробному изложению свойств оценок МНК и способов проверки их значимости.

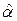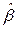Несложно показать, что оценки и полученные МНК по (2.8) с учетом ограничений (2.3)-(2.5) являются линейными несмещенными оценками и обладают наименьшими дисперсиями (являются эффективными) в классе линейных оценок (теорема Гаусса-Маркова).

Для вычисления интервальных оценок a, b предполагаем нормальное распределение случайной величины u. Для получения интервальных оценок a, b оценим дисперсию случайного члена 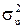по отклонениям e_i. В качестве оценки дисперсии ошибки 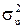возьмем величину:

. (2.12)

Вычислим величину

,

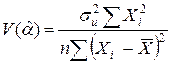и - стандартную ошибку коэффициента регрессии a.

Статистика

,

имеет t-распределение Стьюдента. Так как 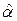несмещенная оценка, то для заданного 100(1–e)% уровня значимости доверительный интервал для a суть:

, (2.13)

где t_e,n-2 – табличное значение t распределения для (n-2) степеней свободы и уровня значимости e.

Вычислим величину

,

и - стандартную ошибку[2] коэффициента регрессии b.

Статистика

,

имеет t-распределение Стьюдента. Так как 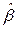несмещенная оценка, то для заданного 100(1–e)% уровня значимости доверительный интервал для b суть:

, (2.14)

где t_e,n-2 – табличное значение t распределения для (n-2) степеней свободы и уровня значимости e.

Проверим гипотезу о равенстве нулю коэффициента a, т.е.

H₀: a=0.

С учетом статистики для a=0, имея в виду формулу для , получим:

. (2.15)

Если вычисленное по (2.15) значение t будет больше t_e для заданного критического уровня значимости e, то гипотеза H₀ о равенстве нулю коэффициента a отклоняется, если же t<t_e, то H₀ принимается.

Аналогично для проверки гипотезы о равенстве нулю коэффициента b, т.е.

H₀: b=0

рассчитаем статистику:

. (2.16)

Если вычисленное по (2.16) значение t будет больше t_e для заданного критического уровня значимости e, то гипотеза H₀ о равенстве нулю коэффициента b отклоняется, если же t<t_e, то H₀ принимается.

Заметим, что формула (2.12) может быть упрощена и записана в виде:

. (2.17)

Пример. Приведем расчеты для нашего примера в табл. 2.1. По формуле (2.17) рассчитаем дисперсию ошибки:

=(1282345–(–2,91)×3861–0,9276×1394495)/10=4,6948 или =2,1667.

Найдем доверительный интервал для a по первой из формул (2.13):

a=.

По таблице t-распределения находим

t_0,05;10=2,228 и a=-2,91±2,228×2668,219/747,0743.

Откуда a=-2,91±7,798 или -10,7£a£4,9.

С вероятностью 0,95 истинные значения a находятся в интервале 10,7£a£4,9.

Аналогично найдем доверительный интервал для b по первой из формул (2.14): b==0,9276±0,022 и 0,91£b£0,95.

Кроме того по экономическому смыслу переменных примера следует ожидать, что 0£b£1. Поскольку доверительный интервал не включает 0 и 1, то результаты регрессии соответствуют гипотезе 0£b£1.

Проверим гипотезу о равенстве нулю коэффициента b, т.е. H₀: b=0.

Рассчитаем t-статистику по формуле (2.16):

t=0,9276×/2,1667=92,328.

Табличное значение t_0,01;10=3,169, так как t>t_0,01;10, то гипотеза о том, что b=0 отклоняется. Можно говорить о том, что коэффициент b значимо отличен от нуля.Ñ

Разложим общую вариацию значений Y около их выборочного среднего на составляющие (см. рис. 2.1):

. (2.18)

Сумма квадратов отклонений от среднего в выборке равна сумме квадратов отклонений значений , полученных по уравнению регрессии, от выборочного среднего плюс сумма квадратов отклонений Y от линии регрессии .

Первую связывают с линейным воздействием изменений переменной X и называют "объясненной".

Вторая составляющая является остатком и называется "необъясненной" долей вариации переменной Y.

Отметим, что долю дисперсии, объясняемую регрессией, в общей дисперсии результативной переменной Y характеризует коэффициент детерминации, определяемый по формуле (2.10), которая может быть преобразована с учетом (2.18) к виду:

.

Предположим, что мы хотим проверить гипотезу об отсутствии линейной функциональной связи между X и Y, т.е. H₀: b=0.

Иначе говоря, мы хотим оценить значимость уравнения регрессии (2.6) в целом. Для проверки гипотезы сведем необходимые вычисления в таблицу (табл. 2.3).

Соотношение

(2.19)

удовлетворяет F - распределению Фишера с (1, n-2) степенями свободы. Критические значения этой статистики F_e для уровня значимости e затабулированы.

Если F>F_e, то гипотеза об отсутствии связи между переменными Y и X отклоняется, в противном случае гипотеза Н₀ принимается и уравнение регрессии не значимо.

 

Таблица 2.3