Нелинейная регрессия
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Различают два класса нелинейных регрессий:
1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например:
– полиномы разных степеней
; (2.24)
– равносторонняя гипербола – 
; (2.25)
– полулогарифмическая функция – 
. (2.26)
2. Регрессии, нелинейные по оцениваемым параметрам, например:
– степенная – 
; (2.27)
– показательная – 
; (2.28)
– экспоненциальная – 
. (2.29)
Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции.
Парабола второй степени 
приводится к линейному виду с помощью замены: 
. В результате приходим к двухфакторному уравнению 
, оценка параметров которого при помощи МНК приводит к следующей системе уравнений:
А после обратной замены переменных получим:
(2.30)
Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую.
Равносторонняя гипербола 
может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы y.
Гипербола приводится к линейному уравнению простой заменой: 
. Система линейных уравнений при применении МНК будет выглядеть следующим образом:
(2.31)
Аналогичным образом приводятся к линейному виду зависимости: 
, 
и другие.
Равносторонняя гипербола и полулогарифмическая кривая используют для описания кривой Энгеля (математическое описание взаимосвязи доли расходов на товары длительного пользования и общих сумм расходов (или доходов)). Уравнения, в которых входят 
, применяются в исследованиях урожайности, трудоемкости сельскохозяйственного производства.
Регрессии, нелинейные по оцениваемым параметрам, делятся на два типа: внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и внутренне нелинейные (к линейному виду не приводятся).
К внутренне линейным моделям относятся, например, степенная функция – 
, показательная – 
, экспоненциальная – 
, логистическая – 
, обратная – 
.
Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры. К внутренне нелинейным моделям можно, например, отнести следующие модели: 
, 
.
В эконометрических исследованиях при изучении эластичности спроса от цены широко используется степенная функция 
, которая приводится к линейному виду логарифмированием:
;
;
,
где 
. Т.е. МНК мы применяем для преобразованных данных:
(2.32)
Параметр b1 определяется непосредственно из системы, а параметр b0 - потенцированием величины lnb0.
Аналогичным образом приводятся к линейному виду зависимости: , .
Приведем к линейному виду логистическую модель 
. Обратив обе части равенства, получим: 
. После вычитания 1 имеем: 
. Прологарифмировав обе части равенства по натуральному основанию, получим уравнение линейной формы 
или
,
где 
и 
.
Широкое использование степенной функции связано с тем, что параметр 
в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. Коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:
, (2.33)
где 
- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора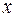 
, то обычно рассчитывается средний коэффициент эластичности.
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии (табл. 2.2).