Интерполяционный полином Лагранжа

Пусть имеется функциональная зависимость y=f(x), для которой нам известны отдельные точки (x_i,y_i), i=0,1,2,…,n. Многочлен y=a₀+a₁x+a₂x²+…+a_nxⁿ, график которого проходит через все данные точки, называется интерполяционным многочленом. Определение этого многочлена по методу Лагранжа начнем с простейших случаев.

Случай 1. Через одну точку (x₀ ,y₀), как известно, можно провести пучок прямых

y=y₀+b(x-x₀) (2.1)

(а также вертикальную прямую x=x₀).

Действительно, уравнение прямой с угловым коэффициентом b имеет вид y=a+bx, при этом должно выполняться равенство y₀=a+bx₀. Вычитая второе равенство из первого, получим уравнение y-y₀=b(x-x₀), равносильное уравнению (2.1).

Случай 2. Через две различные точки (x₀,y₀), (x₁,y₁) проходит одна и только одна прямая. Если x₀ ¹x₁, то ее уравнение имеет вид

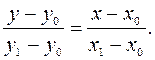(2.2)

Оно получается почленным делением уравнения y-y₀=b(x-x₀) на равенство y₁-y₀=b(x₁-x₀).

Уравнение (2.2) можно привести к виду

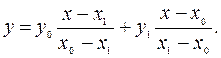(2.3)

Вместе с тем можно непосредственно убедиться в том, что уравнение (2.3) определяет линейную зависимость между величинами y и x и что графиком этой зависимости является прямая линия, которая проходит через точки (x₀,y₀) и (x₁,y₁).

Случай 3. Многочлен второй степени (квадратичная функция), график которой проходит через три точки (x₀,y₀), (x₁,y₁), (x₂,y₂), представляется в виде

Заметим, что дроби при величине y_i (i=0,1,2) обращаются в единицу, если x=x_i и равны нулю при x=x_k (k¹ i).

Случай «n+1». Теперь ясно, что интерполяционный полином Лагранжа n-ой степени, график которого проходит через n+1 точку (x_i,y_i), i=0,1,2,…,n, можно записать в виде

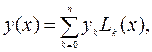
где

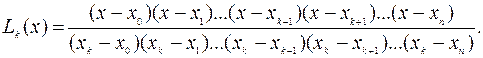
При этом функция L_k(x) равна 1 при x=x_k и равна нулю в остальных узлах x_j (j¹k).

Заметим, однако, что в эконометрике необходимость в использовании интерполяционного многочлена степени выше второй встречается крайне редко. Как правило, предполагается, что эмпирические данные (x_i,y_i) соответствуют какой-нибудь простой зависимости между переменными, например, линейной, но содержат ошибки измерений, вследствие чего точки (x_i,y_i) не лежат на одной прямой (рис.5).

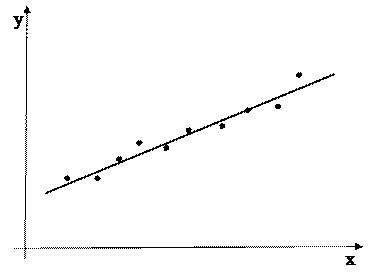
Рис.5. Расположение эмпирических данных по отношении к линейной зависимости.