ОШИБКИ СПЕЦИФИКАЦИИ
Построение экономической модели включает в себя спецификацию ее соотношений, выбор переменных, входящих в соотношение, определение математической функции, входящей в каждое соотношение. В данном пункте мы рассмотрим второй элемент.
Если точно известно, какая переменная должна быть включена в уравнение, то наша задача состоит в определении коэффициентов, построении доверительных интервалов, проверке различных гипотез. На практике мы никогда не можем быть уверены, что уравнение специфицировано правильно. Что случится, если мы включим в уравнение переменные, которых там быть не должно, и что случится, если мы не включим в уравнение переменные, которые там должны присутствовать. Свойства оценок коэффициентов в значительной степени зависят от правильности спецификации модели.
Ошибки спецификации бывают двух видов:
1) невключение в уравнение существенной объясняющей переменной;
2) включение в уравнение переменной, которая не должна там присутствовать.
3) неправильный выбор формы зависимости между переменными, мы предположили, что модель линейная, а она может быть более сложной.
1. Влияние отсутствия в уравнении переменной, которая должна быть включена.
Рассмотрим ситуацию для случая двух переменных.
Истинная модель выглядит следующим образом:  . Но мы не уверены в значимости Z, поэтому оцениваем «короткую» модель:
. Но мы не уверены в значимости Z, поэтому оцениваем «короткую» модель:  . По методу наименьших квадратов вычисляем
. По методу наименьших квадратов вычисляем 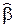 :
:

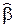 - несмещенная оценка b, если M
- несмещенная оценка b, если M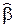 = b. Посчитаем, чему равно M
= b. Посчитаем, чему равно M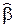 :
:



Таким образом, получаем в числителе:


Итак,  .
.
Таким образом, мы получили смещенную оценку. Оценка будет несмещенной в двух случаях:
1)  ;
;
2) X и Z статистически независимы.
Наша оценка будет завышать или занижать истинное значение коэффициента в зависимости от знака смещения.
Интуитивное объяснение.
Предположим, что b и g положительны, а X и Z положительно коррелированны, тогда с увеличением X
1) Y будет иметь тенденцию к росту, поскольку b положителен;
2) Z будет иметь тенденцию к увеличению, поскольку X и Z положительно коррелированны;
3) Y получит дополнительное ускорение из-за увеличения Z, поскольку g положительно.
Другими словами, изменение Y будет преувеличивать влияние текущих значений X, т. к. отчасти они будут связаны с изменениями Z. Т.е. часть изменения Y за счет изменения Z будет приписано X.
Однако смещение оценок коэффициентов здесь – не единственная неприятность. Что будет с оценками дисперсий?
 - в короткой регрессии (без доказательства).
- в короткой регрессии (без доказательства).
 - в длинной регрессии (без доказательства).
- в длинной регрессии (без доказательства).
Таким образом,  , т. е.
, т. е. 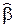 - смещенная оценка, но обладает меньшей дисперсией.
- смещенная оценка, но обладает меньшей дисперсией.
Что будет с оценкой  -
-  ? Оказывается, что в случае, если мы не включаем в регрессию существенную переменную, эта оценка будет смещенной. Поскольку
? Оказывается, что в случае, если мы не включаем в регрессию существенную переменную, эта оценка будет смещенной. Поскольку  участвует во многих статистических тестах, то используя их для проверки гипотез, мы можем получить ложные выводы.
участвует во многих статистических тестах, то используя их для проверки гипотез, мы можем получить ложные выводы.
Итак, в случае невключения объясняющих переменных, МНК-оценка короткой регрессии смещена, и обладает меньшей дисперсией, чем у оценки в длинной регрессии. Оценка дисперсии ошибки имеет неотрицательное смещение.
2. Включение несущественных переменных.
Теперь у нас ситуация противоположная предыдущей. Истинная модель выглядит следующим образом:  , а мы оцениваем «длинную» регрессию
, а мы оцениваем «длинную» регрессию  . Таким образом, включая в уравнение несущественную переменную, мы не учитываем информацию о том, что коэффициент при Z равен нулю. Следует всегда ожидать, что неучитывание всей информации о модели потере эффективности оценок. Т. е. в нашем случае дисперсия оценки в «длинной» регрессии будет больше, чем дисперсия оценки коэффициента при Х в истинной модели, поскольку мы вынуждены по тем же самым наблюдениям оценивать два параметра вместо одного. Тем не менее, оценки «длинной» регрессии останутся несмещенными.
. Таким образом, включая в уравнение несущественную переменную, мы не учитываем информацию о том, что коэффициент при Z равен нулю. Следует всегда ожидать, что неучитывание всей информации о модели потере эффективности оценок. Т. е. в нашем случае дисперсия оценки в «длинной» регрессии будет больше, чем дисперсия оценки коэффициента при Х в истинной модели, поскольку мы вынуждены по тем же самым наблюдениям оценивать два параметра вместо одного. Тем не менее, оценки «длинной» регрессии останутся несмещенными.
Потеря эффективности не случится, если переменные Х и Z некоррелированны. Потеря эффективности приводит к тому, что мы с большей трудностью отвергаем гипотезу о незначимости коэффициента, тем не менее оценка дисперсии b останется несмещенной.
Выводы здесь мы приводить не будем. 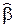 и
и  - несмещенные оценки, но ее дисперсия больше, чем в правильной модели, т. е. точность оценки ухудшается.
- несмещенные оценки, но ее дисперсия больше, чем в правильной модели, т. е. точность оценки ухудшается.
Рисунок с графиками плотностей распределения.
3. Неправильный выбор функциональной зависимости.
Еще одна ошибка спецификации происходит, когда исследователь решает оценить линейную модель, в то время как истинная регрессионная модель нелинейная. Пример:  , а оцениваем мы модель
, а оцениваем мы модель  . Приведенная выше ситуация является частным случаем ситуации с пропущенными переменными. Выбор линейной модели, в то время как истинная модель нелинейная может привести к смещенности и несостоятельности оценок регрессии. Поэтому исследователи часто используют полиномиальную регрессию как тест на нелинейность в объясняющих переменных.
. Приведенная выше ситуация является частным случаем ситуации с пропущенными переменными. Выбор линейной модели, в то время как истинная модель нелинейная может привести к смещенности и несостоятельности оценок регрессии. Поэтому исследователи часто используют полиномиальную регрессию как тест на нелинейность в объясняющих переменных.
Итак, мы с вами рассмотрели теоретические аспекты включения лишних или невключения нужных переменных в уравнение. Что же делать на практике, когда мы никогда точно не знаем, какие переменные входят в модель, а какие нет. В таких ситуациях используют различные эвристические процедуры отбора регрессоров.