Методы устранения гетероскедастичности.

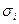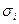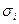В том случае, если было бы известно значение ( огрубл. - стандартная ошибка для ), то достаточно было бы разделить каждое наблюдение на и мы бы устранили гетероскедастичность, т. к. в это случае стандартное отклонение - это есть

Теоретическая дисперсия равна постоянной величине, следовательно, гетероскедастичность отсутствует.

- в этом уравнении отсутствует гетероскедастичность, т. к. дисперсия постоянна, следовательно, можно найти несмещенные оценки и

Данное уравнение называется «взвешенным» уравнением регрессии.

В связи с тем, что 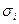не известна, находим такую переменную, которая пропорциональна .

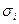, гетероскедастичность можно устранить.

Нужно поделить на Z_i:

При выполнении теста Спирмена или Голдфенда-Квандта в качестве

В случае если закономерность изменения стандартных отклонений от факториального признака Х подчиняется более сложной зависимости, обнаруживается с помощью теста Глейзера, для устранения гетероскедастичности в качестве Z_i берется теоретическое значение модуля