Сечение шара плоскостью
Если шар пересекать плоскостью, то в сечении всегда получается окружность. Эта окружность может спроецироваться:
- в прямую, если секущая плоскость перпендикулярна к плоскости проекций;
- в окружность с радиусом, равным расстоянию от оси вращения шара до очерка, если секущая плоскость параллельна какой-либо плоскости проекций;
- в эллипс, если секущая плоскость не параллельна ни одной из плоскостей проекций.
Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную какой-либо плоскости проекций, и построить окружность, на которой находится эта точка
На рисунке 42 показано построение проекций линии сечения шара фронтально проецирующей плоскость.
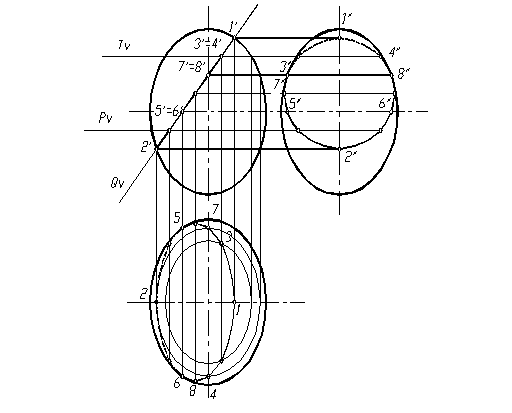
Рис. 42
Построение начинаем с определения характерных точек. Точки 1 и 2 находятся на фронтальном очерке шара (главном меридиане). Эти точки – концы малой оси эллипса, а также самая высокая и самая низкая точки. Их горизонтальные и профильные проекции находятся на соответствующих окружностях шара, которые на горизонтальной и профильной плоскостях совпадают с осями. Точки 3 и 4 находятся на профильном очерке шара (профильном меридиане) и служат для определения видимости на профильной плоскости проекций. Горизонтальные проекции этих точек находятся по фронтальным и профильным. Точки 5 и 6 находятся на горизонтальном очерке шара (экваторе) и служат для определения видимости на горизонтальной плоскости проекций. Профильные проекции этих точек находим по горизонтальным и фронтальным проекциям. Точки 7 и 8 принадлежат концам большой оси эллипса. Они строятся следующим образом. Вначале найдена фронтальная проекция точки 0', центра окружности сечения, как середина отрезка 1'2', затем ее горизонтальная проекция точка 0. Отрезки 0¢1¢ и 0'¢2' на фронтальной проекции равны истиной величине радиуса этой окружности. На горизонтальной проекции диаметр окружности изображается без искажения, поэтому откладываем отрезки 07 и 08, равные 0'1'. Для точного построения линии сечения необходимо найти несколько дополнительных точек. Для их построения используются вспомогательные секущие плоскости (например, плоскости горизонтального уровня T и P, которые в сечении дают окружность на горизонтальной плоскости. Полученные точки соединяют плавной кривой с учетом их видимости.