Обработка результатов измерений на основе закона Гаусса

Пусть истинное значение измеряемой величины X, а результаты измерений представляют собой ряд отсчетов x₁, x₂,…,x_N.

Пусть наблюдаемые значения имеют нормальное распределение .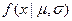

Вероятность того, что все отсчеты попадут в бесконечно малый интервал 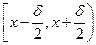равна произведению вероятностей того, что каждый отсвет попадет в этот интервал

.

Чем больше P, тем с большей вероятности наблюдаемые значения группируются вокруг истинного значения. Функция 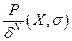называется правдоподобием эксперимента.

Правдоподобие максимально в случае, когда

и

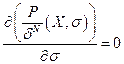
Первое условие можно записать как

,

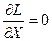где

,

что достигается при

.

Из последнего следует, что

,

т.е. выборочное среднее значение есть максимально правдоподобная оценка истинного значения измеряемой величины.

Второе условие

или .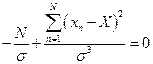

Следовательно

.

т.е. максимально правдоподобная оценка стандартного квадратического отклонения равна выборочному среднему квадратическому отклонению отсчетов от истинного значения.

Величина

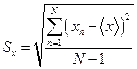
называется средним квадратическим отклонением одиночного наблюдения, которое дает максимально правдоподобную оценку стандартного среднеквадратического отклонения, т.е.

.

Выборочное среднее квадратическое отклонение среднего S­_<x>­­ равно

.

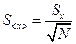Если имеются две независимые точечные оценки <x>₁ и <x>₂ одного и того же истинного значения с дисперсиями s₁ и s_2­, то

,

при этом

.

Доверительным интервалом для m называется интервал 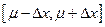в который с вероятностью . Вероятность a называется доверительной вероятностью.