Числовые характеристики генеральной совокупности

Наряду с функцией распределения, наиболее полно характеризующей случайную величину, ее генеральную совокупность, существует ряд чисел, характеризующих случайную величину в некотором частном отношении. К ним относятся математическое ожидание и дисперсия.

Математическое ожидание М[X] есть среднее взвешенное значение случайной величины Х :

М[X] = , (3.14)

где f(x) - плотность распределения Х.

Дисперсия D[X] определяется формулой:

D[X] = M[X - M[X]]² (3.15)

или

D[X] = 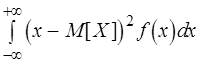. (3.16)

Дисперсия характеризует разброс значений Х относительно ее математического ожидания. Наряду с дисперсией часто рассматривают среднее квадратическое отклонение

s = , (3.17)

размерность которого совпадает с размерностью случайной величины Х.

В случае нормального закона распределения задание математического ожидания М[X] = mи дисперсии s² полностью определяет свойства случайной величины.

Для многих других распределений существенными являются моменты более высоких порядков, такие как коэффициент асимметрии Г₃ и эксцесс Г₄. Первый из них (Г₃) характеризует степень асимметричности распределения случайной величины Х относительно математического ожидания, а второй (Г₄) - указывает на островершинность (плосковершинность) распределения. К ним мы будем обращаться по мере надобности. Здесь же ограничимся их формальным определением:

 

Г₃ = M[X - M[X]]³ / s³ (3.18)

и

Г₄ = {M[X - M[X]]⁴/s⁴ } - 3 . (3.19)

 

Вычитание числа 3 в выражении для Г₄ связано с тем, что для нормального распределения {M[X - M[X]]⁴/s⁴ }= 3. Таким образом, распределения более островершинные, чем нормальные, имеют положительный эксцесс, а распределения менее островершинные, чем нормальное, имеют отрицательный эксцесс.