В результате такой замены мы получили алгебраическое уравнение

1.16

Если в уравнении (1.15) вместо функции времени у(t) и х(t) ввести функции х(р) и у(р) комплексного переменного р=α±jβ , поставив условием что записанные функции связаны отношением

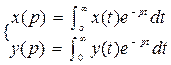1.17

то оказывается что дифференциальное уравнение, содержащие х(t) и у(t) равносильно алгебраическому уравнению вида

1.18

Следует отметить, что трансформация дифференциального уравнения в представленное алгебраическое возможно только при нулевых начальных условиях. И это преобразование в математике называют преобразованием Лапласа. Функции х(р) и у(р) называют изображениями функций х(t) и у(t), а сами функции х(t) и у(t) называют оригиналами функций х(р) и у(р).

Переход от искомой функции у(t) к изображению у(р) называют прямым преобразованием Лапласа, и обозначают

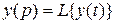1.19

Переход же от изображения у(р) к оригиналу у(t) называют обратным преобразованием Лапласа

1.20

Из сравнения уравнений (1.18) и (1.16) видно, что обе формы записи совпадают, из чего следует, что оператор дифференцирования отождествляется с комплексной переменной р при нулевых начальных условиях.

Использование операторной формы представления уравнений позволяет избежать решения дифференциальных уравнений путем решения системы алгебраических уравнений. Нахождение оригиналов по изображениям можно провести используя либо справочные таблицы, либо формулу разложения.

Взяв за основу формулу (1.18) можно найти отношение

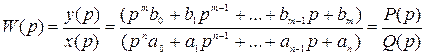1.21

Передаточной функцией W(р) называют отношение изображения по Лапласу выходной величины к изображению входной величины при нулевых начальных условиях.

Из уравнения (1.21) можно записать

1.22

Многочлен, фигурирующий в знаменателе передаточной функции называется характеристическим многочленом, а в случае приравнивания его у нулю уравнение называется характеристическим.

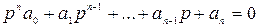1.23

Корни характеристического уравнения называют полюсами передаточной функции. Корни многочлена, расположенного в числителе передаточной функции, называют нулями передаточной функции.

§1.14. Понятие о типовых входных сигналах (воздействиях).

Оценку динамических свойств САУ, т.е. их поведение в переходных режимах можно выполнить различными методами. Решение динамического уравнения, которым описывается звено или система при заданных начальных условиях также отображает их динамику. Оно представляет переходный процесс звена или системы во времени. Для сравнения различных динамических свойств различных элементов рассматривают их переходные процессы, при нулевых начальных условиях и типовых входных воздействий.

Начальные условия – это значение выходной величины, а также всех ее производных в момент времени равное нулю, при условии, что до этого времени внешнее воздействие отсутствовали. Эти начальные условия являются нулевыми, т.к. y(t₀)=y´(0)=…=yⁿ(0)=0.

В качестве типовых входных воздействий принимают определенные формы воздействий, наиболее удобные с точки зрения их математического описания, практической реализации и описания реакции звена на эти воздействия. Иными словами, входное воздействие должно быть простым, не затрудняющим решение уравнения и соответствовать самому тяжелому режиму работы системы из числа встречающихся при ее эксплуатации.

Различают типовые входные воздействия, описываемые следующими функциями:

1. ступенчатой

2. импульсной

3. гармонической

Первые две функции представляют собой временные характеристики звена или системы, а последняя – частотные характеристики.

1. Единичное ступенчатое воздействие.

Оно описывается единичной ступенчатой функцией:

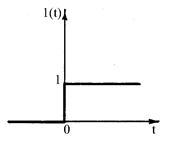а) "Включение" 1(t)

1.24

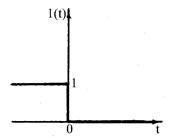б) "Отключение" 1(t)

1.25

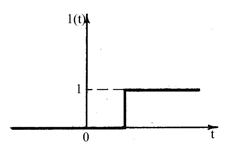в) "Включение с задержкой"

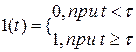1.26

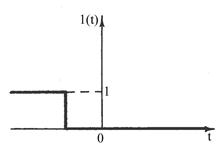г) "Отключение с задержкой"

1.27

2. Импульсное воздействие (единичный импульс).

Импульсное воздействие описывается единичной импульсной функцией d - Дирака (d(t)) является математической идеализацией короткого импульса, площадь которого равна единице, при его длительности равной нулю и амплитуде равной +¥:

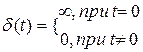1.28

Свойство d(t): площадь этой функции равна 1:

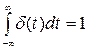1.29

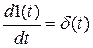1.30

3. Гармоническое воздействие.

Такое воздействие описывается гармонической функцией вида:

1.31

Если к звену или системе приложено воздействие, отличающегося от ступенчатого или импульсного, то его представляют в виде суммы последовательных импульсных или ступенчатых воздействий на звено или систему. Реакция звена или системы на такое воздействие может быть получено с использованием интеграла Дюамеля.

§1.15. Временные характеристики.

К временным характеристикам относятся:

1. Переходная функция – реакция звена или системы на единичную ступенчатую функцию при нулевых начальных условиях, называется переходной функцией, которую обозначают как h(t) и при x=1(t) имеем:

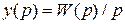1.32

Или переходя от изображения к оригиналу:

1.33

Графическое изображение переходной функции называется переходной характеристикой звена. Покажем наиболее распространенные переходные характеристики:

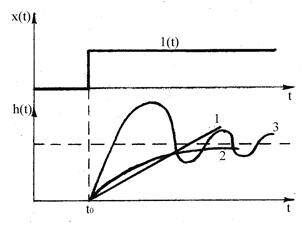1. линейная, установившаяся.

2. апериодическая.

3. колебательная, затухающая.

2. Переходная импульсная функция (функция веса или весовая функция)

Нормальная реакция звена на импульсную функцию называется импульсной переходной функцией или функцией веса, и обозначается w(t). Между импульсной переходной функцией и переходной функцией существует связь:

1.34

1.35

Между передаточной функцией и импульсной переходной функцией существует связь:

1.36

1.37

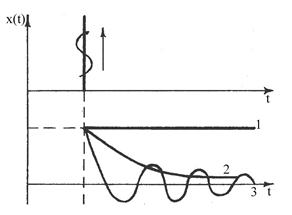
Графическое изображение весовой функции называют импульсной переходной характеристикой звена или системы.

§1.16. Частотные характеристики.

Кроме описания элементов и систем управления временными характеристиками и передаточными функциями в теории автоматического управления также используют и частотные характеристики. Для получения частотных характеристик на вход элемента или системы подают гармонично изменяющийся сигнал. Если на вход подать сигнал в виде гармонической функции то реакция в установившемся режиме также будет гармонической функции, у которой частота остается равной входной, а амплитуда и фаза в процессе передачи изменятся.

Изменение амплитуды и фазы зависят как от свойств звена в системе, так и от частоты гармонического входного воздействия.

Отношение амплитуды выходного сигнала к амплитуде входного, в зависимости от частоты называется амплитудно-частотной характеристикой (АЧХ) звена или системы:

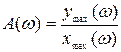1.38

Разность фаз колебаний, в зависимости от частоты называют фазочастотной характеристикой (ФЧХ) звена или системы:

1.39

Частотные характеристики звена или системы зависят только от их свойств, но не зависят от амплитуды и фазы входных гармонических воздействий. Чтобы проследить взаимосвязь между частотными характеристиками или динамическими уравнениями представим входные и выходные воздействия в следующем виде:

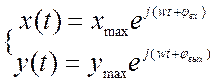1.40

Возьмем производные от рассматриваемых воздействий:

Представим полученное выражение системы (1.40) в уравнение (1.15) и в результате будем иметь выражение вида:

1.41

Взяв отношение выходного сигнала ко входному получим выражение, напоминающее передаточную функцию, но записанной через частотные характеристики

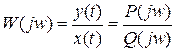1.42

Выражение (1.42) называют частотной характеристикой линейной САУ или что эквивалентно комплексной частотной функции. Функция W(jw) получается из передаточной функции путем подстановки в последнюю вместо оператора Лапласа произведение jw. Функция W(jw), при каждом значении w является комплексной величиной и поэтому может быть представлена в показательной форме как:

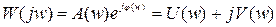1.43

где А(w) – модуль функции W(jw);

j(w) – аргумент частотной функции W(jw).

Функцию W(jw) также принято называть частотной передаточной функцией или частотным передаточным коэффициентом.

Годограф вектора W(jw), при изменении частоты w от 0 до +¥ называют амплитудно-фазовой характеристикой (АФХ или АФЧХ).

Частотные характеристики связаны друг с другом следующими соотношениями:

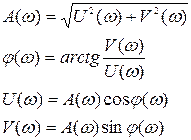1.44

Частотные характеристики элементов или системы можно находить аналитическим путем или используя экспериментальные данные. Покажем внешний вид частотных характеристик: