Свойства корреляционных функций

для ст. сл. пр. с эрг. гипот.

Начальное значение корреляционной функции равно среднему значению квадрата случайного процесса:

Из (1)

(11)

2. Конечное значение корреляционной функции равно квадрату среднего значения случайного процесса:

(12)

Чем больше t, тем меньше связанны случайные величины X(t₁) и X(t₂). При t®величины X(t₁) и X(t₂) можно считать независимыми. Отсюда, учитывая, что для независимых случайных величин

и , можно записать

В чем разница между (11) и (12) на примере

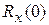
x(t)=t 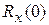(11)

(12)

3.Значение корреляционной функции при любом t не может превышать ее начального значения, т.е.

(13)

Рассмотрим неравенство

Находим среднее значение по времени от обеих частей последнего неравенства

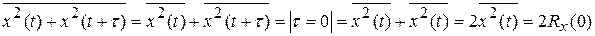
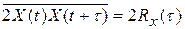(см.(1))

Отсюда

4. Корреляционная функция есть четная функция от t , т.е.

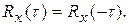(14)

Вытекает из определения

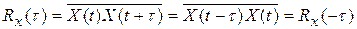( см. (1))

5. Корреляционная функция суммы Z(t)=X(t)+G(t) определяется выражением

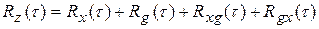(15)

Из свойства математического ожидания имеем

Для взаимной К.Ф. справедливо

5. Корреляционная функция постоянной величины X(t)=A₀

(16)

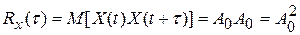
7. Если , то

Для гармонической функции

(17)

от j - не зависит. Указывает на наличие скрытой периодичности.

Для периодической функции справедливо

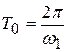- период X(t)

Тогда

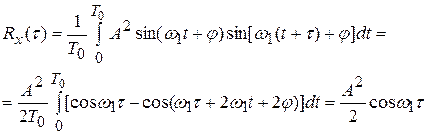
8.Корреляционная функция временной периодической функции, разлагаемой в ряд Фурье

имеет, на основании предыдущей, вид

(18)

9. Корреляционная функция стационарного случайного процесса, на который наложена периодическая составляющая с частотой , так же будет содержать периодическую составляющую той же частоты.

 

R_X(t)

 

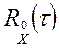
t

 

 

- корреляционная функция случайной составляющей

Для выявления периодической составляющей надо определить корреляционную функцию для больших t , когда случайный сигнал слабо коррелирован. Малый уровень полезного сигнала на фоне больших помех.

10.Типичная корреляционная функция стационарного случайного процесса с неравным нулю средним значением , не содержащего скрытых периодичностей имеет вид.

 

R_X(t)

 

 

 

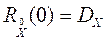
Характерные точки графика

По определяют

1) ср. знач.

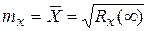
С.К. значение

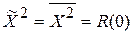
Диспер.

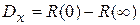
С.К.О.

Если среднее значение случайного процесса равно нулю , то его типичная корреляционная функция совпадает с центрированной корреляционной функцией. В этом случае ее можно апроксимировать следующим аналогичным выражением:

, .

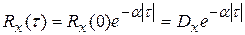X(t) R_X(t)

a)

σ_X = const R_X(0)=D_X

t

б) X(t)

a₂>a₁

t t

 

 

Сравнение а) и б) . Корреляционная функция случайного процесса с тонкой структурой (менее инерц.) убывает быстрее.

Иначе, чем более высокие частоты присутствуют в случайном процессе, тем быстрее убывает соответствующая корреляционная функция.

Иногда встречается корреляционная функция вида

R_X(t)

 

t

 

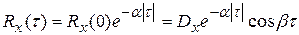(20)

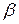- резонансная частота “нерегулярная точка”

Такие корреляционные функции имеют случайные процессы типа турбулентности атмосферы, углового мерцания цели.

11. Чем слабее связь между предыдущим X(t) и последующим X(t+t) значениями случайного процесса, тем быстрее убывает корреляционная функция .

Время , при котором имеет место неравенство , где

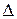- достаточно малая величина, называется временем (интервалом) корреляции случайного процесса.

Обычно 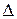=0,05 – 5% трубка

12. Случайный процесс, в котором отсутствует связь между предыдущими и последующими значениями, называется чисто случайным процессом или белым шумом.

Для него 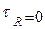(21)

R_X(t)

t

, где

, т.е. ему соответствует бесконечно большая мощность и он не реален. Но в качестве приближения к реальному белый шум используется.

Б.Ш. это стационарный случайный процесс с постоянной на всех частотах спектральной плотностью мощности. Термин Б.Ш. подчеркивает аналогию с белым светом, у которого в пределах видимого диапазона интенсивность всех спектральн. сост. приб. одинак.

Теорема Винера-Хинчина

К.Ф.

Равна 0 всюду, кроме точки 0.

Средн. мощн. его неогран. велика

Некоррелир. мгнов. значений такого сигн. означает бескон. больш. скор. измен. его во времени . Как бы мало не было t , сигнал за это время может измен. на любую наперед задан. величину.

В природе не существует, но им заменяют реальные достаточно широкополосные случайные процессы, в тех случаях, когда полоса пропускания цепи на которую воздействует случайный сигнал , оказывает существенно уже эффективной ширины спектр шума.

При решении практических задач вводят нормированную корреляционную функцию

(22)

.

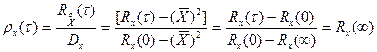При t=0 это удобно.

Иногда вводится в рассмотрение нормированная взаимная корреляционная функция

(23)

причем имеет место