Зависимость константы равновесия от температуры

Зависимость константы равновесия от температуры можно получить, дифференцируя по T уравнение (14) как сложную функцию в изобарных условиях:

или

. (16)

 

Преобразуем выражение (16) с учетом уравнения изотермы (14):

, (17)

где .

Таким образом, уравнение (17) примет вид

. (18)

Решая уравнение (18) относительно , получаем уравнение:

,

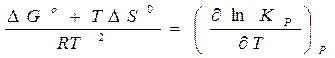или . (19)

Аналогичным образом можно вывести выражение и для зависимости К_С от температуры:

или . (20)

Уравнения (19) и (20) называют уравнениями изобары и изохоры химической реакции в дифференциальной форме, соответственно.

Из этих уравнений следует, что влияние температуры на константу равновесия определяется знаком теплового эффекта.

 

Если реакция эндотермическая, т.е.

, то

и с повышением температуры константа равновесия будет расти, равновесие будет смещаться в сторону продуктов реакции.

Если реакция экзотермическая, т.е.

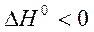, то

то с повышением температуры константа равновесия будет уменьшаться, равновесие будет смещаться в сторону реагентов. Эти качественные выводы о влиянии температуры на химическое равновесие согласуются с принципом Ле Шателье – Брауна.

При интегрировании уравнения изобары необходимо знать температурную зависимость энтальпии . Если расчеты равновесий проводятся в небольшом температурном интервале, можно принять, что энтальпия реакции постоянна. Тогда интегрирование уравнения (19) в пределах от Т₁ до Т₂ дает возможность рассчитать ΔН⁰ реакции, зная константы равновесия при двух различных температурах:

. (21)

Уравнение (21) также позволяет по известным величинам ΔН⁰ реакции и константы равновесия при одной температуре, рассчитать константу равновесия при другой температуре.

Неопределенное интегрирование уравнения (19) приводит к уравнению прямой линии:

,

и дает возможность определить ΔН⁰ реакции графическим способом из угла наклона прямой: .