Общие сведения о сопряжениях

В очертаниях различных геометрических форм часто встречаются плавные переходы от одной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, как правило, дуги окружности называется сопряжением.Построение сопряжений основано на следующих положениях геометрии.

Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной t к окружности (рис. 16, а). Радиус окружности r, проведенный в точку касания К, перпендикулярен к касательной прямой.

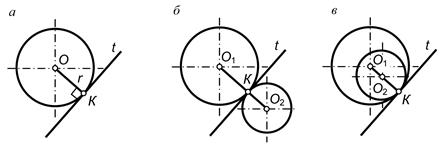
Рис. 16

 

Переход от одной окружности к другой окружности в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную. Точка касания К и центры окружностей O₁ и О₂ лежат на одной прямой. Если центры окружностей лежат по разные стороны от касательной t, то касание называется внешним (рис. 16, б); если центры O₁ и О₂ находятся по одну сторону от общей касательной — соответственно внутренним (рис. 16, в).

В теории сопряжений применяются следующие термины (рис. 17):

· центр сопряжения — точка О, равноудаленная от сопрягаемых линий;

· точки сопряжения К₁и К₂ — точки касания двух сопрягаемых линий;

· дуга сопряжения К₁К₂— это дуга окружности, с помощью которой выполняется сопряжение;

· радиус сопряжения R — это радиус дуги сопряжения.

 

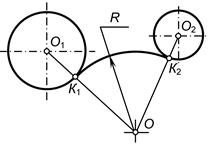
Рис. 17

 

В общем случае построение сопряжения двух линий при заданном радиусе сопряжения состоит из следующих этапов:

1) построение множества точек, находящихся на расстоянии радиуса сопряжения от первой из сопрягаемых линий;

2) построение множества точек, находящихся на расстоянии радиуса сопряжения от второй из сопрягаемых линий;

3) определение на пересечении центра сопряжения;

4) определение точки сопряжения на первой из сопрягаемых линий;

5) определение точки сопряжения на второй из сопрягаемых линий;

6) проведение дуги сопряжения в интервале между точками сопряжения.

Рассмотрим на примерах основные случаи сопряжений.