Многомерные случайные величины

 

Многие экономические показатели определяются несколькими факторами, являясь по сути многомерными СВ. Например, объем продукции растениеводства в сельском хозяйстве может быть охарактеризован уровнем механизации – Х1, численностью работников – Х2, количеством внесенных минеральных удобрений на единицу площади – Х3, количеством осадков в период вегетации – Х4 и качеством почвы – Х5 [1].

Для описания n-мерной СВ Х1, Х2, … Хn (n-мерного случайного вектора Х = (Х1, Х2, … Хn)) вводятся понятия совместной вероятности, совместной функции распределения и совместной плотности вероятностей. Далее, для простоты изложения, будем рассматривать двумерную СВ (n = 2, случайная точка на плоскости), при этом все основные понятия могут быть перенесены на случай n > 2.

В двумерном случае для СВ (X, Y) совместная вероятность определяется соотношением:

P(x, y) = P(X = x, Y = y). (1.21)

Тогда совместная функция распределения F(x, y) определится равенством:

F(x, y) = P(X < x, Y < y). (1.22)

Свойства функции F(x, y) аналогичны свойствам функции распределения одномерной СВ.

Совместной плотностью вероятностей непрерывной двумерной СВ (Х, Y) называется вторая смешанная частная производная ее функции распределения:

. (1.23)

Тогда 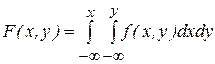и вероятность попадания СВ (X, Y) в область D равна .

Условным законом распределения одной из составляющих двумерной СВ (X, Y) называется закон ее распределения, вычисленный при условии, что другая ее составляющая примет определенное значение. В частности, условные плотности вероятностей fy(x) и fx(y) определяются по формулам:

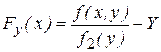примет значение у

(1.24)

примет значение х,

где f1(x) и f2(y) – плотности вероятностей СВ Х и Y.

Числовые характеристики условных законов распределений определяются как условные математические ожидания Мх(Y) и Му(Х) и условные дисперсии Dx(Y) и Dy(X). Они находятся по формулам раздела 1.2, в которых вместо вероятностей событий или плотностей вероятности используются условные вероятности или условные плотности распределения.

Одной из важных задач экономического анализа является обоснование влияния конкретных факторов на исследуемый экономический показатель и установление степени их взаимосвязи друг с другом. Для анализа степени взаимосвязи СВ (степени зависимости между СВ) обычно используют различные моменты распределений, ковариацию (совместное изменение) и коэффициент корреляции [16].

Ковариацией (корреляционным моментом) СВ Х и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий :

Cov(X, Y) = M[(X – M(X)) · (Y – M(Y))] = M(X · Y) – M(X) · M(Y). (1.25)

Кроме обозначения Cov(X, Y), достаточно часто используется обозначение σху.

Если Х и Y независимые СВ, то M(X, Y) = M(X) · (M(Y) и Cov(X, Y) = 0.

Ковариация характеризует наличие положительной (переменные изменяются в одном направлении) или отрицательной (переменные изменяются в разных направлениях) связи между СВ. Ковариация является размерной величиной, что затрудняет ее использование для определения силы (строгости) зависимости между рассматриваемыми СВ. Для устранения данных недостатков вводится относительная мера взаимосвязи – коэффициент корреляции.

Коэффициентом корреляции СВ Х и Y называют отношение их ковариации к произведению средних квадратических отклонений :

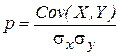
. (1.26)

Основные свойства коэффициента корреляции:

1. -1 £ р £ 1.

2. ρ = 0, если СВ Х и Y независимы.

3. Если |р| = 1, то Y = a + b · X, т. е. между СВ Х и Y существует линейная функциональная зависимость.

Из независимости СВ Х и Y следует их некоррелируемость (ρ = 0). Обратное утверждение неверно. Для расчета дисперсий суммы (разности) коррелированных СВ Х и Y следует использовать формулы :

D(X ± Y) = D(X) + D(Y) ± 2Cov(X, Y)

(1.27)

D(X ± Y) = D(X) + D(Y) ± 2ρ · σx · σy.

Очевидно, что в случае независимости СВ последние слагаемые в этих формулах обращаются в ноль.