И показательное (экспоненциальное) распределение

 

Закон распределения дискретной СВ Х, которая может принимать любые целые неотрицательные значения 0, 1, 2, …, m (бесконечное, но счетное множество значений), описываемый формулой:

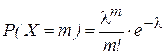(1.18)

носит название закона Пуассона.

Математическое ожидание и дисперсия для СВ, распределенных по закону Пуассона, равны: М(Х) = λ, D(X) = λ.

Закон Пуассона может являться законом распределения вероятностей в экономических процессах с относительно редкими рассматриваемыми событиями. Таким процессам должно быть присуще одно общее характерное свойство – число возможных исходов (например, значений курсов валют) очень велико, а число фактически происходящих событий (биржевые курсы), напротив, очень мало. Закон распределения Пуассона также находит широкое применение в теории массового обслуживания.

Аналогом закона Пуассона для непрерывных СВ служит показательный (экспоненциальный) закон распределения, плотность вероятности которого имеет вид:

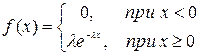. (1.19)

Показательный закон имеет параметр λ > 0 и числовые характеристики:

М(Х) = 1/λ, D(X) = 1/λ².

Функция распределения СВ Х (интегральная функция) показательного закона

. (1.20)

Показательное распределение находит применение в теории надежности и в широком смысле описывает время t безотказной работы системы, при этом число λ интерпретируется как интенсивность отказов (среднее число отказов в единицу времени). Функция распределения F(t) = P(T < t) = 1 - e^λt определяет вероятность отказа системы (элемента системы) за время t. Тогда величина R(t) = e^-λt называется функцией надежности и определяет вероятность безотказной работы элемента системы за время t.