Распределение Стьюдента

 

Рассмотрим стандартную нормальную СВ U ~ N(0,1) и независимую от нее СВ V, распределенную по закону χ² с ν = n степенями свободы (обозначается V ~ 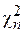). Тогда распределение случайной величины

(1.16)

называется распределением Стьюдента (псевдоним английского химика и статистика Госсета) или t-распределением с n-степенями свободы (t_n).

При n > 2 M(t) = 0 и D(t) = n/n - 2. График функции плотности вероятности СВ, имеющей распределение Стьюдента, является симметричной кривой относительно оси ординат (рис. 1.6) [11].

 

 

 

Рис. 1.6.

 

С увеличением числа степеней свободы распределение Стьюдента приближается к стандартному нормальному закону и практически при n > 30 можно считать t-распределение приближенно нормальным. Таблица критических точек распределения Стьюдента для различных значений уровня значимости α и числа степеней свободы ν (t_α,ν) представлена в Приложении 4.