Приведение системы сходящихся сил к равнодействующей

Покажем, что система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна векторной сумме всех этих сил и проходит через точку пересечения их линий действия.

Пусть задана система сходящихся сил , приложенных к абсолютно твердому телу (рис.2.1.а).

 

 

Согласно следствию из первых двух аксиом перенесем точки приложения сил вдоль их линий действия до точки O пересечения этих линий (рис.2.1.б).

Получим систему сил, приложенных в одной точке и эквивалентную исходной системе сходящихся сил. Сложим теперь силы и . На основании третьей аксиомы, получим их равнодействующую . Затем, сложив полученную силу с силой , получим .

Очевидно, что результат есть равнодействующая трех сил.

 

Осуществляя последовательно сложение сил, получим равнодействующую для всей системы сходящихся сил как

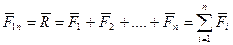(2.1)

что и требовалось доказать.

Пространственный многоугольник, построенный последовательным присоединением начала последующего вектора силы к концу предыдущего с замыканием контура равнодействующей, называется силовым многоугольником.

Если для нахождения равнодействующей при помощи силового многоугольника используются правила геометрии и тригонометрии, то такой способ нахождения равнодействующей называется геометрическим. В случае плоской системы сходящихся сил можно воспользоваться плоским чертежом, откладывая силы в некотором масштабе; равнодействующая может быть определена непосредственным измерением на чертеже. Такой способ ее нахождения называется графическим.

Наиболее общим способом определения модуля и направления равнодействующей является аналитический способ, суть которого в проецировании равенства (2.1) на оси выбранной координатной системы, например декартовой. В этом случае проекции равнодействующей, ее модуль и направляющие косинусы рассчитываются, как

 

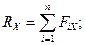
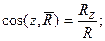(2.2)