Ход решения задачи

 

Метод контурных токов выводится из метода непосредственного применения законов Кирхгофа путём исключения уравнений, составляемых по первому закону Кирхгофа.

Указанная процедура достигается за счёт введения обобщённых переменных, так называемых контурных токов, относительно которых составляются уравнения по второму закону Кирхгофа. Полученные уравнения решаются относительно контурных токов. Затем токи в ветвях выражаются через найденные контурные токи.

Порядок расчёта рассмотрим на примере схемы рис. 3.1.

Определим число уравнений, составляемых по второму закону Кирхгофа

m – (n – 1) = 6 – (4 – 1) = 3,

 

где n – число узлов; m – число ветвей.

Число уравнений равно числу неизвестных контурных токов. В нашем случае – три уравнения. Обозначим контурные токи , и . Выбираем направление контурных токов совпадающих с направлением вращения часовой стрелки. Номера контуров совпадают с индексами контурных оков. Отметим, что во второй, четвёртой и пятой ветвях текут по два контурных тока. Составляем систему из трёх уравнений по второму закону Кирхгофа относительно контурных токов. При этом учтём падение напряжения на резисторных элементах от каждого контурного тока, текущего по нему.

Рис. 3.1. Расчётная схема сложной электрической цепи

Направление обхода контуров выберем совпадающим с направлением соответствующего контурного тока. Первое уравнение соответствует первому контуру, второе – второму и т.д.

В результате, система имеет вид

 

.

 

После решения этой системы уравнений действительные токи ветвей определяются по найденным контурным токам:

 

, , , , , .

 

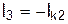Отметим, что при определении токов , и учитывалось, что контурный ток, совпадающий с током в ветви, берётся со знаком «+», не совпадающий – со знаком «–». При этом значения контурных токов подставляются в формулы со своим знаком.