Контактная разность потенциалов
Основные носители заряда при переходе через p и n области перехода должны преодолевать потенциальный барьер. В состоянии термодинамического равновесия диффузионный ток основных носителей заряда Jоp и Jоn уравновешен дрейфовым током неосновных носителей заряда Jнp и Jнn, и суммарный ток через pn-переход равен нулю.
Если Φn есть работа выхода электронов из электронного полупроводника, а Φp – из дырочного, то величина потенциального барьера будет определяться выражением:
 (48)
(48)
или
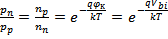 , (49)
, (49)
где Vbi – общепринятое обозначение контактной разности потенциалов, которое в случае pn-перехода имеет собственное название встроенный или диффузионный потенциал (built in potential).
Т.о., контактная разность потенциалов на pn-переходе тем больше, чем сильнее легированы n- и p-области полупроводника. Из (49) в состоянии термодинамического равновесия непосредственно следует
 . (50)
. (50)
Пусть к переходу приложено внешнее напряжение V, минус – к электронному полупроводнику, а плюс – дырочному, т.е. к pn-переходу приложено напряжение в прямом смещении. Поскольку сопротивление слоя объемного заряда высокое, то падение напряжения в основном будет в этой области. Вследствие этого высота барьера снижается на величину qV по сравнению с равновесным состоянием. Понижение потенциального барьера приведет к увеличению потока основных носителей, т.к. большее число электронов из n-области будет переходить в p-область и большее число дырок из p-области в n-область, а поток неосновных носителей заряда останется практически неизменным. В результате во внешней цепи будет протекать ток, равный разности токов основных и неосновных носителей заряда и направленный от p-области к n-области, т.е. J=Jон-Jнн. В n-области, появившиеся избыточные неосновные носители заряда – дырки Δp создадут в первый момент вблизи контакта положительный объемный заряд, который за очень короткое время определяемое временем максвелловской релаксации будет скомпенсирован зарядом основных заряда – электронов, которые под действием электрического поля, созданного избыточными дырками, будут подтянуты в количестве Δn из глубины n-области, а в n-область избыточные электроны поступят из внешней цепи. Т.о., во всех частях электронного полупроводника будет соблюдаться электронейтральность, но в приконтактной области перехода концентрация будет повышена на величину Δn=Δp по сравнению с равновесным состоянием. Введение в полупроводник избыточных носителей заряда с помощью pn-перехода при подаче на него прямого смещения, где эти носители являются неосновными, называется инжекция носителей заряда. Соответственно,
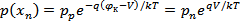 , (51)
, (51)
откуда следует, что концентрация избыточных дырок в n-области при x=xn равна:
 . (52)
. (52)
Совершенно аналогично
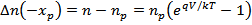 . (53)
. (53)
Если внешнее напряжение приложено в обратном направлении, т.е. плюс к электронному полупроводнику, потенциальный барьер повышается и увеличивается толщина области пространственного заряда. В этом случае из (38) следует, что при большом отрицательном V концентрация дырок при x=xn быстро стремиться к нулю. Аналогично, концентрация электронов при x=-xp также стремится к нулю. Такой режим работы pn-перехода называется режимом экстракции носителей заряда. При обратном включении pn-перехода ток основных носителей заряда будет меньше, чем при равновесном состоянии, а ток неосновных носителей практически не изменится. Поэтому суммарный ток через pn-переход будет направлен из n-области к p-области и с увеличением обратного напряжения стремится к некоторой величине, называемой током насыщения.
Связь распределения электрического потенциала, концентрацией легирующей примеси и концентрациями свободных носителей заряда осуществляется в уравнении Пуассона, которое в одномерном случае имеет вид:
 , (54)
, (54)
где ND(x), NA(x) – концентрации донорной и акцепторной примеси, n(x,V), p(x,V) – концентрации электронов и дырок, εs, ε0 – относительная диэлектрическая проницаемость полупроводника и диэлектрическая проницаемость вакуума (ε0=8.854·10-14 [ф/см]), ρ – пространственная плотность заряда, V – электростатический потенциал.
Если принять, что при термодинамическом равновесии вся легирующая примесь является полностью ионизированной, то n≈(ND+-NA-) и p=ni2/n. В квазинейтральных областях pn-перехода (где область пространственного заряда отсутствует), поэтому
 (55)
(55)
и
 . (56)
. (56)
В случае резкого перехода концентрациями подвижных носителей заряда n и p в области пространственного заряда пренебрегают и уравнение Пуассона (54) приобретает вид:
 (57)
(57)
или
 для
для  (58)
(58)
 для
для  . (59)
. (59)

Рис.8. Обедненная область в случае резкого pn-перехода.
Интегрируя (58)-(59) один раз, находим выражение для электрического поля
 для
для  (60)
(60)
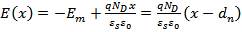 для
для  , (61)
, (61)
где Em – максимальное значение электрического поля, которое достигается при x=0 и равно
 . (62)
. (62)
Еще раз интегрируя уравнение Пуассона, получим распределение потенциала и величину диффузионного потенциала V(x):
 , (63)
, (63)
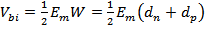 , (64)
, (64)
где W – ширина обедненной области. Исключая Em из (64) с использованием (62), получим для резкого pn-перехода в равновесном случае
 . (65)
. (65)
В случае прямого смещения pn-перехода величина обедненной области уменьшается:
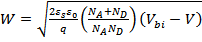 , (66)
, (66)
а в случае обратного смещения (-V) увеличивается:
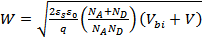 . (67)
. (67)
Более точное выражение для ширины области пространственного заряда получается, если кроме концентрации ионизированной примеси дополнительно учесть вклад основных носителей заряда, т.е. положить ρ≈-q[NA-p(x)] в p-области перехода и ρ≈-q[ND-n(x)] в n-области перехода. Ширина обедненной области в таком приближении вычисляется по тем же формулам (53)-(54) если заменить Vbi на Vbi-2kT/q. Поправочный член появляется из-за наличия двух «хвостов» распределения основных носителей заряда. Каждый из них вносит поправку kT/q. Сама поправка представляет дипольный момент неточности в распределении, равной разности между истинным распределением и распределением в резком переходе. Соответственно, (66) и (67) переписываются в виде:
 (68)
(68)
 . (69)
. (69)