Абсолютное значение погрешности

en absolute value of an error

fr valeur absolue d´une erreur

Значение погрешности без учета ее знака (модуль погрешности)

Примечание - Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности

9.11 относительная погрешность измерения;

относительная погрешность

de relativer Fehler (einer Messung)

en relative error

fr erreur relative

Погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.

Примечание - Относительную погрешность в долях или процентах находят из отношений

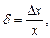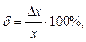или (9.4)

где Dх - абсолютная погрешность измерений; х - действительное или измеренное значение величины

9.12 рассеяние результатов в ряду измерений;

рассеяние результатов;

рассеяние

de Streuung

en dispersion

fr dispersion

Несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.

Примечания

1 Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.

2 Оценками рассеяния результатов в ряду измерений могут быть:

размах,

средняя арифметическая погрешность (по модулю),

средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение),

доверительные границы погрешности (доверительная граница или доверительная погрешность)

9.13 размах результатов измерений;

размах

Оценка R_n рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из п измерений), вычисляемая по формуле

R_n = x_max - x_min, (9.5)

где х_max и x_min - наибольшее и наименьшее значения физической величины в данном ряду измерений.

Примечание - Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер

9.14 средняя квадратическая погрешность результатов единичных измерений в ряду измерений;

средняя квадратическая погрешность измерений;

средняя квадратическая погрешность;

СКП

en experimental standard deviation

fr écart-type experimental

Оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемая по формуле

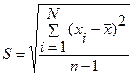, (9.6)

где х_i - результат i-го единичного измерения;

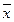- среднее арифметическое значение измеряемой величины из п единичных результатов.

Примечание - На практике широко распространен термин среднее квадратическое отклонение - (СКО). Под отклонением в соответствии с формулой (9.6) понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В Метрологии, как отмечено в 9.1, это отклонение называется погрешностью измерений. Если в результаты измерений введены поправки на действие систематических погрешностей, то отклонения представляют собой случайные погрешности. Поэтому с точки зрения упорядочения совокупности терминов, родовым среди которых является термин «погрешность измерения», целесообразно применять термин «средняя квадратическая погрешность». При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений

9.15 средняя квадратическая погрешность результата измерений среднего арифметического;

средняя квадратическая погрешность среднего арифметического;

средняя квадратическая погрешность;

СКП

en experimental standard deviation of the mean

fr écart-type experimental de la moyenne

Оценка случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле

, (9.7)

где S - средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений; п - число единичных измерений в ряду

9.16 доверительные границы погрешности результата измерений;

доверительные границы погрешности;

доверительные границы

Наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

Примечания

1 Доверительные границы в случае нормального закона распределения вычисляются как ± , ± , 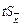где , - средние квадратические погрешности, соответственно, единичного и среднего арифметического результатов измерений; t - коэффициент, зависящий от доверительной вероятности Р и числа измерений п.

2 При симметричных границах термин может применяться в единственном числе - доверительная граница.

3 Иногда вместо термина доверительная граница применяют термин доверительная погрешность или погрешность при данной доверительной вероятности