Дифференциальные уравнения

Название	Вид	Решение
Первого порядка с разделяющимися переменными	Уравнение, приводящееся к виду: q(x)dx = g(y)dy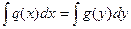
Однородные первого порядка	P(x,y)dx + Q(x,y)dy = 0 , где P(x,y) и Q(x,y) – однородные функции одинакового m-ого измерения ( P(λx,λy) = λmP(x,y); Q(λx,λy) = λm Q(x,y) )	Замена y = ux , где u – функция от x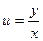
В полных дифференциалах	P(x,y)dx + Q(x,y)dy = 0, где	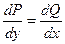U(x,y) = C , где dU = P dx + Q dy
Линейные первого порядка	a(x) y' + b(x) y = c(x) или   y' + p(x) y = q(x)	Метод вариации произвольных постоянных: Решить сначала однородное уравнение: v' + p(x) v = 0 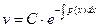, затем найти С = u(x) ,подставив в исходное уравнение.
Подстановкой y = uv [u' + p(x) u] v + v'u = q(x) u' + p(x) u = 0
Бернулли		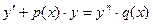Подстановка: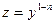
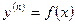
Уравнения п-ого порядка, допускающие понижение порядка (неполные).		Замен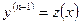а , тогда 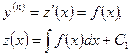повторяя эту операцию (п-1) раз, получится у(х).
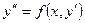
Неполные, второго порядка	Не содержащие явно у	Замена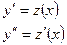
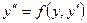
Не содержащие явно x	Замена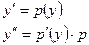