Метрологические основы аналитической химии

Хемометрика (хемометрия) – химическая дисциплина, которая занимается применением математических и статистических мето­дов для планирования и выбора оптимальных условий проведения хи­мического эксперимента и аналитического измерения, а также полу­чения максимума информации из химических данных. Термин предложен в 1971 г. шведским ученым С. Волдом.

Методы хемометрики используются на всех основных этапах химического анализа.

Приближенные вычисления и значащие цифры.Некоторые из численных величин, полученных эксперименталь­ным путём, могут быть известны абсолютно точно (например, число таблеток, взятых для анализа), другие же (объём раствора, масса на­вески) всегда известны с некоторой неопределённостью. Простейшим способом описания неопределённости численной величины является понятие «значащие цифры».

Значащими называют все достоверные цифры, входящие в со­став численной величины, а также первую, следующую за ними, не­достоверную цифру. Например, в числе 103,2 четыре значащие цифры. 1,0,3 достоверно известны, 2 имеет некоторую неопределенность. Обычно «по умолчанию» недостоверность последней значащей цифры принимается равной ±1. Указанную выше величину можно представить как 103,2±0,1.

При определении числа значащих цифр, входящих в состав чис­ленной величины, используют следующие правила:

• положение запятой не влияет на число значащих цифр.Например, 2035 203,5 20,35 2,035 – имеют одинаковое число значащих цифр – четыре.

• нули, входящие в состав числа, могут быть как значимыми, так и незначимыми.Нули, стоящие в начале числа, всегда незначимы и служат лишь для указания места запятой в десятичной дроби. Например, число 0,01 содержит только одну значащую цифру. Нули, стоящие между цифрами, всегда значимы. Например, в числе 0,508 три значащие цифры. Нули в конце числа могут быть значимы и не значимы. Нули, стоящие после запятой в десятичной дроби, считаются значимыми. Например, в числе 200,0 четыре значащие цифры. Нули же в конце целого числа могут означать значащую цифру, а могут просто указывать порядок величины. Например, в числе 200 значащих цифр может быть одна (2), две (2 и 0), три (2,0 и 0). Чтобы избежать неопределенности, рекомендуется в таких случаях представить число в нормальном виде, т.е. в виде произведения числа, содержащего только значащие цифры на 10ⁿ. Например, если в числе 200 одна значащая цифра, то следует изобразить его как 2·10², если две значащие цифры –2,0·10², если три значащие цифры –2,00·10².

При вычислениях с использованием экспериментально получен­ных величин следует помнить, что в результате расчётов «точность» не должна искусственно повышаться, так как она определяется тем, с какой погрешностью измерены исходные величины, входящие в рас­чётную формулу. Существуют определённые правила, которые в большинстве случаев позволяют избежать ошибок при расчётах.

Сложение и вычитание.Перед проведением данных действий необходимо проводить округление. Принцип округления: если первая цифра, следующая за округляемой, меньше 5, то округленная цифра остается неизменной, если больше 5, то округляемая цифра увеличивается на 1. Если же цифра, следующая за округляемой, точно рана 5, то четную округляемую цифру оставляют без изменений, а нечетную увеличивают на 1. Например, число 10,245 следует округлить до 10,24, а число 10,255 – до 10,26..

Основное правило сложения и вычитания: сумма (или разность) должна содержать столько же десятичных знаков, сколько этих знаков содержится у числа с наименьшим их количеством. Например, при сложении чисел 28,3; 5 и 0,46 значимость определяется недостоверностью числа 5 и, следовательно, сумму чисел 33,76 следует округлить до 34.

Рекомендуется округлять конечный результат после выполнения всех арифметических действий.

Числа, содержащие степени, преобразуют, приводя показатели степеней слагаемых и наибольшему, а затем поступают так же, как и для обычных чисел. Например,

1,03·10²+5,2·10³ = 0,103·10³+5,2·10³ =5,3·10³

Умножение и деление. Строгий подход к определению правильного числа значащих цифр, которое должно остаться в произведении или в частном, пред­полагает сравнение относительных недостоверностей исходных вели­чин и получаемых результатов. В большинстве случаев, однако, мож­но ограничиться следующим правилом: результат деления или ум­ножения должен иметь столько же значащих цифр (не десятич­ных знаков!), сколько их содержится в наименее точно известном числе.Например,10,32 · 0,22 = 2,3.

Другие операции.При возведении в степень, равную n, относительная недостовер­ность результата будет в n раз больше, чем недостоверность исходной величины. При извлечении квадратного корня (n = 1/2) относительная недостоверность уменьшается в два раза, кубического (n = 1/3) - в три раза, поэтому можно, например, считать, что 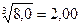и т.д. При взятии десятичного логарифма недостоверность результата составляет примерно 0,43 от относительной недостоверности исходного числа, поэтому при логарифмировании число значащих цифр обычно увеличивают. При потенцировании (взятии антилогарифма) число значащих цифр, на­оборот, уменьшают. Например:

lg 0,01 (или lg 1·10^–2) = -2,0; 10^-2,0 = 0,01 (или 1·10^–2).

Некоторые основные положения математиче­ской статистики, используемые в аналитической химии

Случайной величинойназывается измеряемая по ходу опыта численная характеристика, принимающая одно и только одно воз­можное и наперёд неизвестное значение вследствие действия различ­ных факторов, которые не могут быть заранее учтены. Случайные величины бывают дискретными и непрерывными.

Дискретнойназывают случайную величину, множество воз­можных значений которой конечно либо счётно (т.е. может быть пронумеровано натуральными числами). Непрерывнойназы­вают случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала. Большинство случайных величин, с которыми химик-аналитик сталкивается на практике, являются непрерывными.

Для того, чтобы математически описать случайную величину, необходимо указать множество ее значений и соответствующее случайной величине распределение вероятностей для этого множества (таблично, аналитически или графически).

Функцией распределения случайной величиныназывается функция, определяемая равенством F(x) =P(X≤x), где P(X≤x) – вероятность того, что случайная погрешность Х примет любое значение, которое меньше или равно х.

Функция f(x) называется плотностью вероятности непрерывной случайной величины, если для любых чисел a и b (a>b) выполняется равенство

.

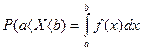Плотность вероятности и функция распределения связаны между собой уравнениями

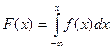
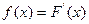
Явления, носящие случайный характер, также как и закономер­ные явления подчиняются определённым законам, с помощью кото­рых можно определить, какова будет вероятность того, что случайная величина примет интересующее нас значение. Распределения вероят­ностей случайных величин могут быть дискретными и непрерывными. Наиболее важным непрерывным распределением вероятностей, ис­пользуемых в аналитической химии, является нормальное распреде­ление.Примерами одномерного нормального распределения являют­ся идеальный хроматографический пик или полоса поглощения в электронном спектре. Плотность вероятности нормально распределённой случайной величины описывается формулой:

.

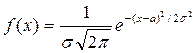Любое нормальное распределение описывается двумя параметрами: параметр а по смыслу является математическим ожиданием случайной величины и характеризует положение графика функции F(x) относительно числовой оси, параметр σ (σ > 0), характеризующий растяжение (сжатие) графика, будучи возведённым в квадрат, равен дисперсии случайной величины. Нормальное распределение с а = 0 и σ = 1 называется стандартным нормальным распределением.

Вероятность попадания значений нормально распределённой случайной величины в интервал a ± 3σ составляет 99,73%, т.е. прак­тически все значения нормально распределённой случайной величины находятся в этом интервале. Это свойство нормального распределения называется «правилом3σ».

Для характеристики случайной величины на практике пользуют­ся выборкой. Выборкойназывается последовательность независимых одинаково распределённых случайных величин. Обозначим результата анализа как случайную величину Х. Проведем в неизменных условиях некоторое количество параллельных анализов одного и того же объекта. У нас получится ряд независимых одинаково распределенных случайных величин x₁ , x₂ ... x_n, например, значений аналитического сигнала. Данный ряд будет представлять собой выборку, при помощи которой можно будет оценить функцию распределения и другие характеристики случайной величины Х. Выборка, пронумеро­ванная в порядке возрастания, т.е. x₁ , x₂ ... x_n, называется вариацион­ным рядом.Сами значения x называются вариантами,а n- объёмом выборки.В таблице приведены основные характеристики, исполь­зуемые для описания выборки.

 

Основные характеристики используемые для описания выборки
Характеристика	Определение понятия	Расчетная формула
выборочное среднее	сумма всех значений серии наблюдений, деленная на число наблюдений
выборочная дисперсия (исправленная)	сумма квадратов отклонений, деленная на число степеней; характеризует рассеяние результатов относительно среднего. Число степеней свободы f=n–1 – число переменных, которые могут быть присвоены произвольно при характеристике данной выборки.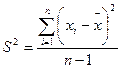
выборочное стандартное отклонение	положительный квадратный корень из выборочной дисперсии; характеризует рассеяние результатов в выборочной совокупности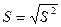
стандартное отклонение выборочного среднего	отношение выборочного стандартного отклонения к положительному квадратному корню из числа наблюдений
относительное стандартное отклонение	отношение выборочного стандартного отклонения к выборочному среднему; характеризует рассеяние результатов в выборочной совокупности
Границы доверительного интервала	интервал, вероятность попадания значений случайной величины в который равна принятой нами доверительной вероятности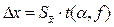

 

Для характеристик малых объемов, взятых из нормально распределенных генеральных совокупностей, используют распределение Стьюдента (t–распределение) (предложено в 1908 г. английским химиком У. Госсетом, он опубликовал свои работы под псевдонимом Student).

Пусть некоторая случайная величина имеет нормальное распределение вероятностей. Для оценки этой случайной величины воспользуемся выборкой объемом n. Чем меньше число степеней свободы (n–1), тем в большей степени выборочные характеристики будут отличаться от характеристик случайной величины. Введем новую случайную величину t.

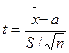или

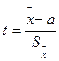
Распределение этой случайной величины называется распределением Стьюдента. Распределением Стьюдента пользуются для характеристики нормально распределенных выборок малых объемов (n<30). Данное распределение зависит только от объёма выборки и не зависит от неизвестных параметров a и σ. При n→∞ распределение Стьюдента переходит в стандартное нормальное распределение. Распределение Стьюдента можно использовать для расчёта до­верительного интервала выборочного среднего (в том случае, если выборка имеет нормальное распределение). Доверительным интер­валомназывается интервал, вероятность попадания значений случай­ной величины в который равна принятой нами доверительной вероят­ности 1–α, где α – уровень значимости (в аналитической практике α=0,05):

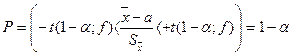
Следовательно, неизвестное математическое ожидание с вероятностью 1–α попадет в такой интервал:

.

 

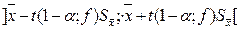Например, если α = 0,05 и f = 5, то доверительный интервал для выборочного среднего равен .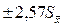

Процесс анализа многостадиен. Каждая стадия вносит опреде­лённый вклад в неопределённость окончательного результата. Перед началом статистической обработки необходимо прове­рить, не содержат ли полученные результаты грубых погрешностей. Измерения, в которых обнаружены такие погрешности, должны быть исключены. Их нельзя использовать при дальнейшей статистической обработке результатов. Существует несколько способов исключения грубых погрешностей. Для исключения промахов при работе с вы­борками малого объёма (n = 4–10) можно воспользоваться величиной Q-критерия (тест Диксона).Экспериментальное значение Q-критерия равно отношению разности выпадающего и ближайшего к нему результата на размах варьирования, т.е. разности наибольшего и наименьшего из результатов выборочной совокупности:

или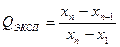

Полученное значение сравнивают с критической (табличной) величиной для Q-критерия. Если оно превышает последнюю, то проверяемый результат является промахом и его необходимо исключить из дальнейших расчетов.

Для выборок больших объемов можно использовать, например, «правило 3σ» – если значение отличается от среднего более, чем на 3 стандартных отклонения, то его можно считать промахом.

Далее для обработки данных используют формулы, указанные в таблице.