Дифракция Френеля и дифракция Фраунгофера

Пусть на пути сферической монохроматической световой волны, идущей от источника P₀, располагается плоский непрозрачный объект с отверстием S, размеры которого велики по сравнению с длиной волны (рис.1). В соответствии с

Рис.1.

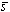принципом Гюйгенса-Френеля для нахождения поля в некоторой точке P необходимо рассмотреть интерференцию волн, идущих от вторичных источников, расположенных в прозрачной части объекта S . При этом амплитуда и фаза сферических волн, приходящих в точку P, зависят от расстояния от источника P₀ до соответствующих участков объекта на поверхности S и от расстояния от этих участков до точки P. В общем случае распределение поля U(P) может быть найдено с помощью интегральной формулы Френеля-Кирхгофа [1]

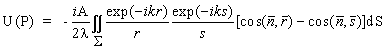
(1)

где l - длина волны;
k = 2p/l - волновое число;
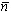- вектор нормали к поверхности объекта;
dS - элемент площади в плоскости объекта;
i - мнимая единица;
A - константа;

интегрирование ведется по открытой поверхности S объекта. В этой формуле член, пропорциональный exp(-ikr)/r, описывает сферическую волну, распространяющуюся из точки P₀ до некоторого вторичного источника, расположенного на поверхности S, член, пропорциональный exp(-iks)/s, - сферическую волну, идущую от вторичного источника до точки наблюдения P, а член 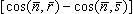описывает изменение амплитуды вторичных волн в зависимости от направления распространения падающей и вторичных волн. Наиболее интересным для рассмотрения является случай, когда характерный линейный размер отверстия bмал по сравнению с расстояниями и 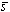от точек P₀ и P до объекта. При этом как множитель 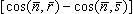, так и член 1/rsизменяются при интегрировании по отверстию S незначительно, и основную роль в вычислении дифракционной картины по формуле (1) играет интеграл от быстро осциллирующего члена exp[-ik(r+s)]. Разложение в ряд этого члена (см. например [1, стр. 417]) позволяет существенно упростить формулу (1).

Явления, описываемые в рамках такого приближения, носят название дифракции Френеля, или дифракции в ближней зоне. При r стремящемуся к бесконечности фронт падающей волны можно считать плоским. Если s стремится к бесконечности, то и вторичные волны, распространяющиеся под некоторым углом j к первоначальному направлению, образуют плоский волновой фронт. Дифракционные явления, наблюдаемые при этих условиях, носят название дифракции Фраунгофера, или дифракции в дальней зоне.

Различие между дифракцией Френеля и дифракцией Фраунгофера становится более наглядным, если ввести понятиезон Френеля. Для этого рассмотрим дифракцию на круглом отверстии радиуса R (рис. 2).

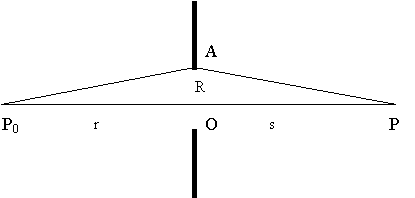
Рис.2.

Пусть источник света P₀ и точка наблюдения Pнаходятся на оси отверстия на расстояниях r и s соответственно. Выделим в плоскости объекта два вторичных источника: первый, расположенный на оси в точке О, и второй, расположенный на краю отверстия в точке А. Нетрудно показать, что свет, идущий из т. P₀ в т. P через вторичный источник О, пройдет путь, равный r+s, а свет, прошедший через вторичный источник А - путь

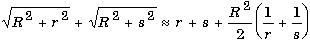Введя обозначение

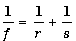
получим выражение для разности хода между двумя путями: 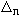. Говорят, что радиус отверстия R равен радиусу n-й зоны Френеля R_n, если разность хода 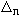, соответствуюшая этому радиусу, составляет n длин полуволн, т.е.

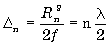
откуда радиус n-й зоны Френеля равен

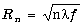Таким образом, размер отверстия, выраженный в количестве открытых зон Френеля, зависит не только от расстоянийr и s, но и от длины волны l источника света. Можно показать, что если число открытых зон Френеля нечетное, то в т. P будет наблюдаться светлое пятно, если же открыто четное число зон Френеля, то в центре картины будет темное пятно. Если объект имеет произвольную форму с характерным размером b (например, длинная шель ширины b), то можно показать, что, если b много меньше радиуса первой зоны Френеля

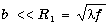то при рассмотрении явления дифракции можно пользоваться приближением Фраунгофера. Если размер объекта составляет одну или несколько зон Френеля, то в этом случае справедливо приближение Френеля. Если же размер объекта велик и составляет десятки и сотни зон Френеля, то явления дифракции на таком объекте практически не проявляются и в этом случае работает приближение гоеметрической оптики.