Дифракция на диске
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна
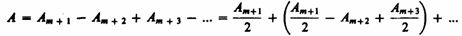
или
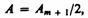
так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.
Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна
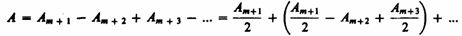
или
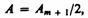
так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается угол т (см. рис. 258) между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.
Зонная пластинка Френеля
Зонная пластинка — плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями, радиус которых совпадает с радиусами зон Френеля. Зонная пластинка «выключает» чётные либо нечётные зоны Френеля, чем исключает взаимную интерференцию (погашение) от соседних зон, что приводит к увеличению освещённости точки наблюдения. Таким образом, зонная пластинка действует как собирающая линза.
Также зонная пластинка представляет собой простейшую голограмму — голограмму точки.
Принцип действи]
Согласно принципу Гюйгенса-Френеля световое поле в некоторой точке пространства является результатом интерференции вторичных источников. Френель предложил оригинальный и чрезвычайно наглядный метод группировки вторичных источников. Этот метод позволяет приближенным способом рассчитывать дифракционные картины, и носит название метода зон Френеля.
Зоны Френеля вводятся следующим образом. Рассмотрим распространение световой волны из точки L в точку наблюдения P. Сферический волновой фронт, исходящий из точки L разобьем концентрическими сферами с центром в точке P и с радиусами z1 + λ/2; z1 + 2 λ/2; z1 + 3 λ/2…
Полученные кольцевые зоны и носят название зон Френеля.
Смысл разбиения поверхности на зоны Френеля состоит в том, что разность фаз элементарных вторичных волн, приходящих в точку наблюдения от данной зоны, не превышает π. Сложение таких волн приводит к их взаимному усилению. Поэтому каждую зону Френеля можно рассматривать как источник вторичных волн, имеющих определенную фазу. Две соседние зоны Френеля действуют как источники, колеблющиеся в противофазе, т.е вторичные волны, распространяющиеся из соседних зон в точке наблюдения будут гасить друг друга. Чтобы найти освещенность в точке наблюдения P нужно просуммировать напряженности электрических полей от всех вторичных источников, приходящих в данную точку. Результат сложения волн зависит от амплитуды и разности фаз. Так как разность фаз между соседними зонами равна π, то можно перейти к суммированию амплитуд.
Амплитуда вторичной сферической волны пропорциональна площади элементарного участка, испускающего эту волну (т.е пропорциональна площади зоны Френеля). Кроме того, она убывает с увеличением расстояния z1 от источника вторичной волны до точки наблюдения по закону 1 / z1 и с ростом угла φ между нормалью к элементарному участку, испускающего волну, и направлением распространения волны.
Можно показать, что площади зон Френеля примерно одинаковы и равны:
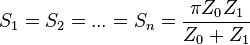 , где Sn — площадь n-ой зоны Френеля, z0 — радиус сферы.
, где Sn — площадь n-ой зоны Френеля, z0 — радиус сферы.
Расстояние z1n от зоны до точки наблюдения медленно растет по линейному закону: z1n = z1 + n λ / 2, где n — номер зоны.
Угол φ также увеличивается при увеличении номера зоны Френеля. Следовательно, амплитуды вторичных волн убывают. Таким образом, можно записать A1 > A2 > A3 > … > An-1 > An > An+1 > …, где An — амплитуда вторичной волны, испущенной n-ой зоной. Амплитуда результирующего светового колебания в точке наблюдения P будет определяться вкладом всех зон. При этом, волна из второй зоны Френеля будет гасить волну из первой зоны (так как они придут в точку P в противофазе), волна из третьей зоны будет усиливать первую волну (так как между ними разность фаз равна нулю), четвертая волна ослабит первую и так далее. Это значит, что при суммировании необходимо учесть, что все четные зоны дадут вклад в результирующую амплитуду одного знака, а все нечетные зоны — противоположного знака. Таким образом, суммарная амплитуда в точке наблюдения равна: A = A1 — A2 + A3 — A4 + …